
【題目】今年是第39個植樹節,我們提出了“追求綠色時尚,走向綠色文明”的倡議.某校為積極響應這一倡議,立即在八、九年級開展征文活動,校團委對這兩個年級各班內的投稿情況進行統計,并制成了如圖所示的兩幅不完整的統計圖. 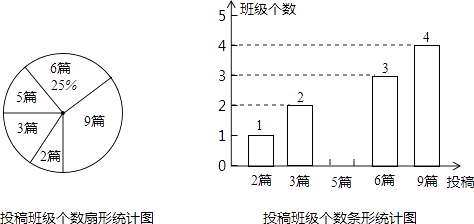
(1)求扇形統計圖中投稿3篇的班級個數所對應的扇形的圓心角的度數.
(2)求該校八、九年級各班在這一周內投稿的平均篇數,并將該條形統計圖補充完整.
(3)在投稿篇數最多的4個班中,八、九年級各有兩個班,校團委準備從這四個班中選出兩個班參加全校的表彰會,請你用列表法或畫樹狀圖的方法求出所選兩個班正好不在同一年級的概率.
【答案】
(1)解:班級總個數為:3÷25%=12(個), ![]() ×360°=60°.
×360°=60°.
故投稿篇數為3所對應的扇形的圓心角的度數為60°
(2)解:投稿5篇的班級數為:12﹣1﹣2﹣3﹣4=2(個),
(2+3×2+5×2+6×3+9×4)÷12=72÷12=6(篇),
將該條形統計圖補充完整為:

(3)解:畫樹狀圖如下:
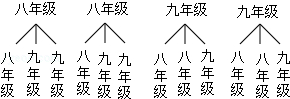 ,
,
總共12種情況,兩班不在同一年級的有8種情況,
所以所選兩個班不是同一年級的概率為:8÷12= ![]()
【解析】(1)根據投稿6篇的班級個數是3個,所占的比例是25%,可求總共班級個數,利用投稿篇數為3的比例乘以360°即可求解;(2)根據加權平均數公式可求該校八,九年級各班在這一周內投稿的平均篇數,再用總共班級個數﹣不同投稿情況的班級個數即可求解;(3)利用樹狀圖法,然后利用概率的計算公式即可求解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC內部的一個動點,且滿足∠PAB=∠PBC,則線段CP長的最小值為( ) 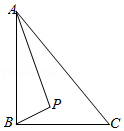
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=4,AD=7,點E,F分別在邊AD、BC上,且B、F關于過點E的直線對稱,如果以CD為直徑的圓與EF相切,那么AE= . 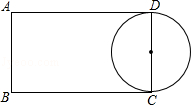
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,∠MON=45°,點P是∠MON內一點,過點P作PA⊥OM于點A、PB⊥ON于點B,且PB=2 ![]() .取OP的中點C,聯結AC并延長,交OB于點D.
.取OP的中點C,聯結AC并延長,交OB于點D.
(1)求證:∠ADB=∠OPB;
(2)設PA=x,OD=y,求y關于x的函數解析式;
(3)分別聯結AB、BC,當△ABD與△CPB相似時,求PA的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=6,點E為BC的中點,將△ABE沿AE折疊,使點B落在矩形內點F處,連接CF,則CF的長為( ) 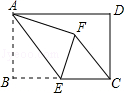
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖甲,在△ABC中,AB=AC,∠BAC=90°.點D為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF. 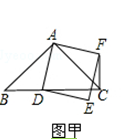
解答下列問題:
(1)當點D在線段BC上時(與點B不重合),如圖甲,線段CF、BD之間的位置關系為 , 數量關系為 .
(2)當點D在線段BC的延長線上時,如圖乙,①中的結論是否仍然成立,為什么? 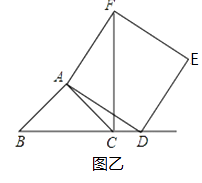
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AB=3cm,現將紙片折疊壓平,使點A與點C重合,折痕為EF,如果sin∠BAE= ![]() ,那么重疊部分△AEF的面積為( )
,那么重疊部分△AEF的面積為( ) 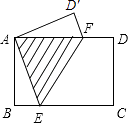
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c的象經過A(﹣1,0)、B(3,0)、N(2,3)三點,且與y軸交于點C.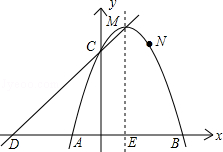
(1)求這個二次函數的解析式,并寫出頂點M及點C的坐標;
(2)若直線y=kx+d經過C、M兩點,且與x軸交于點D,試證明四邊形CDAN是平行四邊形;
(3)點P是這個二次函數的對稱軸上一動點,請探索:是否存在這樣的點P,使以點P為圓心的圓經過A、B兩點,并且與直線CD相切?如果存在,請求出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市種植某種綠色蔬菜,全部用來出口.為了擴大出口規模,該市決定對這種蔬菜的種植實行政府補貼,規定每種植﹣畝這種蔬菜一次性補貼菜農若干元.經調查,種植畝數y(畝)與補貼數額x(元)之間大致滿足如圖1所示的一次函數關系.隨著補貼數額x的不斷增大,出口量也不斷增加,但每畝蔬菜的收益z(元)會相應降低,且z與x之間也大致滿足如圖2所示的一次函數關系. 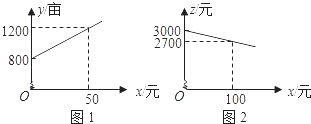
(1)在政府未出臺補貼措施前,該市種植這種蔬菜的總收益額為多少?
(2)分別求出政府補貼政策實施后,種植畝數y和每畝蔬菜的收益z與政府補貼數額x之間的函數關系式;
(3)要使全市這種蔬菜的總收益w(元)最大,政府應將每畝補貼數額x定為多少?并求出總收益w的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com