解:(1)與△AGF相似的有△EGO、△AEO、△DFO;
(2)∵四邊形ABCD是正方形,
∴OA=OD,∠BAO=∠DAO=45°,
在△AEO與△DFO中
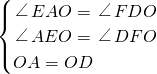
,
∴△AEO≌△DFO(AAS),
∴AE=DF,
∴AE+AF=AD=16;
(3)∵四邊形ABCD是正方形,
∴△OAD為等腰直角三角形,
∴OA=OD=

AD=8

,
∵AG:GO=3:5,
∴AG=3

,GO=5

,
∵△EGO∽△AEO,
∴OE:OA=OG:OE,即OE
2=OA•OG=8

•5

=80,
∴OE=4

,
∵∠EAO=∠EFO=45°,∠EOF=90°,
∴△OEF為等腰直角三角形,
∴EF=

OE=4

,
∵△AGF∽△EGO,
∴AG:EG=FG:OG,即3

:EG=(4

-EG):5

,
解得EG=

,EG=3

(舍去),
∴AF:OE=AG:EG,即AF:4

=3

:

,
∴AF=12,
∴DF=AD-AF=4,
∵DF•DA=DH•DO,
∴DH=
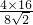
=4

.
分析:(1)根據正方形的性質得到∠EAO=∠FAG=∠FDO=45°,根據同弧所對的圓周角相等得到∠OEG=∠OAF=45°,∠AOE=∠AFO,根據圓周角定理由∠EAF=90°得到EF為⊙O的直徑,則∠EOF=90°,而∠AOD=90°,根據等角的余角相等得到∠AOE=∠DOF,然后利用三角形相似的判定可得到△AGF∽△EGO∽△AEO∽△DFO;
(2)首先可證△AEO≌△DFO,即可得AE=DF,繼而求得AE+AF的值;
(3)根據正方形的性質可判斷△OAD為等腰直角三角形,則OA=OD=

AD=8

,所以AG=3

,GO=5

,再由△EGO∽△AEO,利用相似比可計算出OE=4

,
再判斷△OEF為等腰直角三角形,則EF=

OE=4

,接著由△AGF∽△EGO,利用相似比可先計算EG=

,再計算出AF=12,則DF=AD-AF=4,
然后根據切割線定理計算DH.
點評:此題考查了相似三角形的判定與性質:有兩組角對應相等的兩個三角形相似;相似三角形對應角相等,對應邊的比相等.也考查了全等三角形的判定與性質、圓周角定理和正方形的性質.

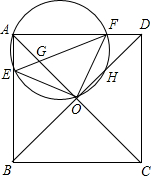 如圖,已知正方形ABCD的對角線AC、BD相交于O,經過A、O的圓分別與AB、AD相交于E、F,EF與AO相交于G,AD=16.
如圖,已知正方形ABCD的對角線AC、BD相交于O,經過A、O的圓分別與AB、AD相交于E、F,EF與AO相交于G,AD=16.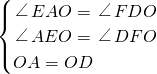 ,
, AD=8
AD=8 ,
, ,GO=5
,GO=5 ,
, •5
•5 =80,
=80, ,
, OE=4
OE=4 ,
, :EG=(4
:EG=(4 -EG):5
-EG):5 ,
, ,EG=3
,EG=3 (舍去),
(舍去), =3
=3 :
: ,
,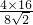 =4
=4 .
. AD=8
AD=8 ,所以AG=3
,所以AG=3 ,GO=5
,GO=5 ,再由△EGO∽△AEO,利用相似比可計算出OE=4
,再由△EGO∽△AEO,利用相似比可計算出OE=4 ,
, OE=4
OE=4 ,接著由△AGF∽△EGO,利用相似比可先計算EG=
,接著由△AGF∽△EGO,利用相似比可先計算EG= ,再計算出AF=12,則DF=AD-AF=4,
,再計算出AF=12,則DF=AD-AF=4,

 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案 (2013•北碚區模擬)如圖,已知正方形ABCD,點E是BC上一點,點F是CD延長線上一點,連接EF,若BE=DF,點P是EF的中點.
(2013•北碚區模擬)如圖,已知正方形ABCD,點E是BC上一點,點F是CD延長線上一點,連接EF,若BE=DF,點P是EF的中點. 如圖,已知正方形ABCD,點E在BC邊上,將△DCE繞某點G旋轉得到△CBF,點F恰好在AB邊上.
如圖,已知正方形ABCD,點E在BC邊上,將△DCE繞某點G旋轉得到△CBF,點F恰好在AB邊上. 如圖,已知正方形ABCD的對角線AC,BD相交于點O,E是AC上的一點,過點A作AG⊥BE,垂足為G,AG交BD于點F.
如圖,已知正方形ABCD的對角線AC,BD相交于點O,E是AC上的一點,過點A作AG⊥BE,垂足為G,AG交BD于點F.