
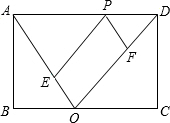
 如圖,已知矩形ABCD的邊長AB=2,BC=3,點Q是BC邊的中點,點P是AD邊上的一個動點,PE∥DQ交AQ于點E,PF∥AQ交DQ于點F.
如圖,已知矩形ABCD的邊長AB=2,BC=3,點Q是BC邊的中點,點P是AD邊上的一個動點,PE∥DQ交AQ于點E,PF∥AQ交DQ于點F.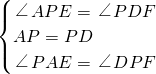


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 如圖,已知矩形DEFG內接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=
如圖,已知矩形DEFG內接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=| 45 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 m/秒的速度移動,如果M、N兩點同時出發,移動的時間為x秒(0≤x≤6).
m/秒的速度移動,如果M、N兩點同時出發,移動的時間為x秒(0≤x≤6).查看答案和解析>>
科目:初中數學 來源: 題型:
 點A運動.
點A運動.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•寧德質檢)如圖,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜邊AC平均分成n段,以每段為對角線作邊與AB、BC平行的小矩形,則這些小矩形的面積和是( )
(2012•寧德質檢)如圖,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜邊AC平均分成n段,以每段為對角線作邊與AB、BC平行的小矩形,則這些小矩形的面積和是( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知矩形ABCD中AB:BC=3:1,點A、B在x軸上,直線y=mx+n(0<m<n<
如圖,已知矩形ABCD中AB:BC=3:1,點A、B在x軸上,直線y=mx+n(0<m<n<| 1 |
| 2 |
| 9 |
| 8 |
| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com