
【題目】“搶紅包”是2015年春節十分火爆的一項網絡活動,某企業有4000名職工,從中隨機抽取350人,按年齡分布和“搶紅包”所持態度情況進行調查,并將調查結果繪成了條形統計圖和扇形統計圖.
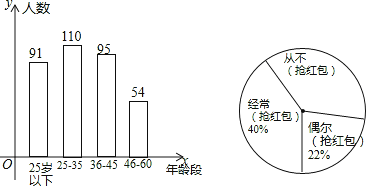
(1)這次調查中,如果職工年齡的中位數是整數,那么這個中位數所在的年齡段是哪一段?
(2)如果把對“搶紅包”所持態度中的“經常(搶紅包)”和“偶爾(搶紅包)”統稱為“參與搶紅包”,那么這次接受調查的職工中“參與搶紅包”的人數是多少?并估計該企業“從不(搶紅包)”的人數是多少?
【答案】(1)25-35之間;(2)217人;1520人.
【解析】試題分析:(1)根據中位數的定義,中位數是大小處于中間位置的數,根據定義即可作出判斷;
(2)利用調查的職工的人數350乘以對應的百分比即可求得“參與搶紅包”的人數;
利用總人數4000乘以“從不(搶紅包)”的比例即可求得“從不(搶紅包)”的人數.
試題解析:(1)這次調查中,如果職工年齡的中位數是整數,那么這個中位數所在的年齡段是25-35之間;
(2)“經常(搶紅包)”和“偶爾(搶紅包)”共占的百分比為40%+22%=62%,
則這次接受調查的職工中“參與搶紅包”的人數是350×62%=217(人);
根據題意得:4000×(1-40%-22%)=1520(人),
則該企業“從不(搶紅包)”的人數是1520人.


科目:初中數學 來源: 題型:
【題目】若關于的x一元二次方程kx2–2x–1=0有兩個不相等的實數根,則k的取值范圍是( )
A. k >–1 B. k >–1且k ≠0 C. k <1 D. k <1,且k ≠0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據媒體報道,我國因環境污染造成的巨大經濟損失,每年高達680000000元,這個數精確到百萬位用科學記數法表示正確的是( )
A. 6.80×107 B. 6.8×108 元 C. 6.80×108元 D. 6.8×106元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一定的條件下,若物體運動的路程s(米)與時間t(秒)的關系式為s=5t2+2t,則當t=4秒時,該物體所經過的路程為( )
A. 28米 B. 48米 C. 68米 D. 88米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c的頂點坐標為M(0,-1),與x軸交于A、B兩點.
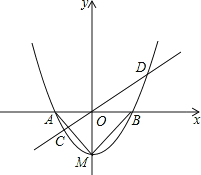
(1)求拋物線的解析式;
(2)判斷△MAB的形狀,并說明理由;
(3)過原點的任意直線(不與y軸重合)交拋物線于C、D兩點,連接MC,MD,試判斷MC、MD是否垂直,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某次體育測試中,九年級一班女同學的一分鐘仰臥起坐成績(單位:個)如下表:
成績 | 45 | 46 | 47 | 48 | 49 | 50 |
人數 | 1 | 2 | 4 | 2 | 5 | 1 |
這此測試成績的中位數和眾數分別為( )
A. 47,49 B. 47.5,49 C. 48,49 D. 48,50
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com