
如圖①, 已知拋物線![]() (a≠0)與
(a≠0)與![]() 軸交于點A(1,0)和點B (-3,0),與y軸交于點C.
軸交于點A(1,0)和點B (-3,0),與y軸交于點C.
(1) 求拋物線的解析式;
(2) 點D的坐標為(-2,0).問:直線AC上是否存在點F,使得△ODF是等腰三角形?若存在,請直接寫出所有符合條件的點F的坐標;若不存在,請說明理由.
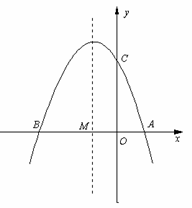
(3) 如圖②,若點E為第二象限拋物線上一動點,連接BE、CE,求△BCE面積的最大值,并求此時E點的坐標.
解: (1)由題知: ![]() 解得:
解得: ![]()
∴ 所求拋物線解析式為: ![]() ……3分
……3分
(2) 存在符合條件的點P, 其坐標為P (-1, 2 )或P(-![]() ,
,![]() )
)
或P(-![]() ,
,![]() )……3分
)……3分
(3)過點E 作EF⊥x 軸于點F , 設E ( a ,-![]() -2a+3 )( -3< a < 0 )
-2a+3 )( -3< a < 0 )
∴EF=-![]() -2a+3,BF=a+3,OF=-a
-2a+3,BF=a+3,OF=-a
∴S四邊形BOCE = ![]() BF·EF +
BF·EF + ![]() (OC +EF)·OF
(OC +EF)·OF
=![]() ( a+3 )·(-
( a+3 )·(-![]() -2a+3) +
-2a+3) + ![]() (-
(-![]() -2a+6)·(-a)
-2a+6)·(-a)
=![]() =-
=-![]()
![]() +
+![]()
∴ 當a =-![]() 時,S四邊形BOCE 最大, 且最大值為
時,S四邊形BOCE 最大, 且最大值為 ![]() .……3分
.……3分
∴S四邊形BOCE-S△ABC =![]() -6=
-6=![]()
∴點E 坐標為 (-![]() ,
,![]() )……1分
)……1分


 優等生題庫系列答案
優等生題庫系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 軸上,CF交y軸于點B(0,2),且其面積為8.
軸上,CF交y軸于點B(0,2),且其面積為8.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com