【題目】某超市促銷活動，將
三種水果采用甲、乙、丙三種方式搭配裝進禮盒進行銷售．每盒的總成本為盒中三種水果成本之和，盒子成本忽略不計．甲種方式每盒分別裝三種水果
；乙種方式每盒分別裝三種水果
．甲每盒的總成本是每千克
水果成本的
倍，每盒甲的銷售利潤率為
；每盒甲比每盒乙的售價低
；每盒丙在成本上提高
標價后打八折出售，獲利為每千克 水果成本的
倍．當銷售甲、乙、丙三種方式搭配的禮盒數量之比為
時，則銷售總利潤率為__________.
【答案】20%．
【解析】
分別設每千克A、B、C三種水果的成本為x、y、z，設丙每盒成本為m，然后根據題意將甲、乙、丙三種方式的每盒成本和利潤用x表示出來即可求解．
設每千克A、B、C三種水果的成本分別為為x、y、z，依題意得：
6x+3y+z=12.5x，
∴3y+z=6.5x，
∴每盒甲的銷售利潤=12.5x20%=2.5x
乙種方式每盒成本=2x+6y+2z=2x+13x=15x，
乙種方式每盒售價=12.5x（1+20%）÷（1-25%）=20x，
∴每盒乙的銷售利潤=20x-15x=5x，
設丙每盒成本為m，依題意得：m（1+40%）0.8-m=1.2x，
解得m=10x．
∴當銷售甲、乙、丙三種方式的水果數量之比為2：2：5時，
總成本為：12.5x2+15x2+10x5=105x，
總利潤為：2.5x2+5x×2+1.2x5=21x，
銷售的總利潤率為
×100%=20%，
故答案為：20%．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，Rt△ABC的頂點B、C的坐標分別為(3，4)、(4，2)，且AB平行于x軸，將Rt△ABC向左平移，得到Rt△A′B′C′．若點B′、C′同時落在函數y=
（x＞0）的圖象上，則k的值為（ ）
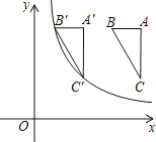
A.2B.4C.6D.8
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2016年某園林綠化公司購回一批香樟樹，全部售出后利潤率為20%．
（1）求 2016年每棵香樟樹的售價與成本的比值．
（2）2017年，該公司購入香樟樹數量增加的百分數與每棵香樟樹成本降低的百分數均為a，經測算，若每棵香樟樹售價不變，則總成本將比2016年的總成本減少8萬元；若每棵香樟樹售價提高百分數也為a，則銷售這批香樟樹的利潤率將達到4a．求a的值及相應的2017年購買香樟樹的總成本．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與雙曲線
交于A點，且點A的橫坐標是4．雙曲線上有一動點C（m，n）, 
.過點A作
軸垂線，垂足為B，過點C作軸垂線，垂足為D，聯結OC．
（1）求
的值；
（2）設
的重合部分的面積為S，求S與m的函數關系；
（3）聯結AC，當第（2）問中S的值為1時，求
的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在初中階段的函數學習中，我們經歷了“確定函數的表達式——利用函數圖象研究其性質一一運用函數解決問題”的學習過程．在畫函數圖象時，我們通過描點或平移的方法畫出了所學的函數圖象．同時，我們也學習了絕對值的意義
．
結合上面經歷的學習過程，現在來解決下面的問題:在函數
中，當
時，
當
時，
．
求這個函數的表達式；
在給出的平面直角坐標系中，請用你喜歡的方法畫出這個函數的圖象；
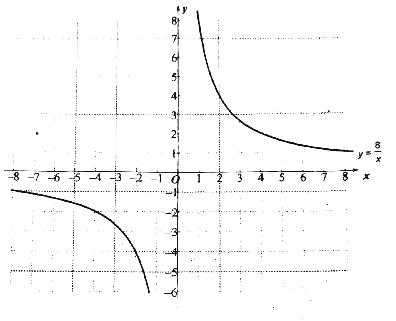
已知函數
的圖象如圖所示，結合你所畫的函數圖象，直接寫出不等式
的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某種電纜在空中架設時，兩端掛起的電纜下垂都近似成拋物線
的形狀，現按操作要求，電纜最低點離水平地面不得小于6米．
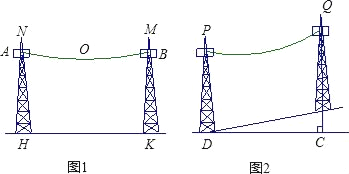
(1)如圖1，若水平距離間隔80米建造一個電纜塔柱，求此電纜塔柱用于固定電纜的位置離地面至少應有多少米的高度？
(2)如圖2，若在一個坡度為1：5的斜坡上，按水平距離間隔50米架設兩固定電纜的位置離地面高度為20米的塔柱．
①求這種情況下在豎直方向上，下垂的電纜與斜坡的最近距離為多少米？
②這種情況下，直接寫出下垂的電纜與地面的最近距離為多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC不動，△ADE繞點A旋轉，連接BE，CD，F為BE的中點，連接AF.
(1)如圖①，當∠BAE＝90°時，求證：CD＝2AF；
(2)當∠BAE≠90°時，(1)的結論是否成立？請結合圖②說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
