
【題目】如圖,![]() 為
為![]() 直徑,
直徑,![]() 是
是![]() 上一點,
上一點,![]() 于點
于點![]() ,弦
,弦![]() 與
與![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() ,使
,使![]() ,
,![]() 交
交![]() 的延長線于點
的延長線于點![]() .過點
.過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求弧
,求弧![]() 的長;
的長;
(3)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)證明見解析;(2)![]() ;(3)6.
;(3)6.
【解析】
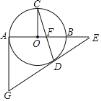
(1)連接OD,如圖,先證明∠3=∠1,再證明∠C=∠4,然后利用∠3+∠C=90°得到∠1+∠4=90°,則OD⊥DE,然后根據切線的判定定理即可得到結論;
(2)由切線的性質得∠OAG=90°,則利用四邊形內角和可計算出∠AOD=130°,然后根據弧長公式可計算出弧![]() 的長;
的長;
(3)設OF=x,則OB=3x,則可表示出BF=2x,再利用∠1=∠2得到ED=EF=2x+4,然后在Rt△ODE中,根據勾股定理得到(3x)2+(2x+4)2=(4+3x)2,再解方程求出x即可得到OB的長.
(1)連接OD.如圖,∵∠1=∠2,而∠2=∠3,∴∠3=∠1.
∵OC⊥AB,∴∠3+∠C=90°,∴∠1+∠C=90°.
∵OC=OD,∴∠C=∠4,∴∠1+∠4=90°,即∠ODE=90°,∴OD⊥DE,∴GE是⊙O的切線;
(2)∵AG為切線,∴AG⊥AB,∴∠OAG=90°,而∠ODG=90°,∴∠AOD=180°﹣50°=130°,∴弧![]() 的長=
的長=![]() =
=![]() π;
π;
(3)設OF=x,則OB=3x,∴BF=2x.
∵∠1=∠2,∴ED=EF=2x+4.
在Rt△ODE中,∵OD2+DE2=OE2,∴(3x)2+(2x+4)2=(4+3x)2,解得:x=2,∴OB=3x=6.


科目:初中數學 來源: 題型:
【題目】為了響應市委和市政府“綠色環保,節能減排”的號召,幸福商場用3300元購進甲、乙兩種節能燈共計100只,很快售完.這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲種節能燈 | 30 | 40 |
甲種節能燈 | 35 | 50 |
(1)求幸福商場甲、乙兩種節能燈各購進了多少只?
(2)全部售完100只節能燈后,商場共計獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校創客小組進行機器人跑步大賽,機器人小![]() 和小
和小![]() 從同一地點同時出發,小
從同一地點同時出發,小![]() 在跑到1分鐘的時候監控到程序有問題,隨即開始進行遠程調試,到3分鐘的時候調試完畢并加速前進,最終率先到達終點,測控小組記錄的兩個機器人行進的路程與時間的關系如圖所示,則以下結論正確的有_________ (填序號).
在跑到1分鐘的時候監控到程序有問題,隨即開始進行遠程調試,到3分鐘的時候調試完畢并加速前進,最終率先到達終點,測控小組記錄的兩個機器人行進的路程與時間的關系如圖所示,則以下結論正確的有_________ (填序號).
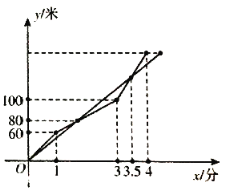
①兩個機器人第一次相遇時間是在第2分鐘;
②小![]() 每分鐘跑50米;
每分鐘跑50米;
③賽程總長200米;
④小![]() 到達終點的時候小
到達終點的時候小![]() 距離終點還有20米.
距離終點還有20米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】制作一種產品,需先將材料加熱達到60 ℃后,再進行操作.設該材料溫度為y(℃),從加熱開始計算的時間為x(min).據了解,當該材料加熱時,溫度y與時間x成一次函數關系;停止加熱進行操作時,溫度y與時間x成反比例關系(如圖).已知該材料在操作加熱前的溫度為15 ℃,加熱5分鐘后溫度達到60 ℃.

(1)分別求出將材料加熱和停止加熱進行操作時,y與x的函數關系式;
(2)根據工藝要求,當材料的溫度低于15 ℃時,須停止操作,那么從開始加熱到停止操作,共經歷了多少時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
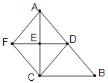
【題目】如圖,在Rt△ABC中,∠ACB=90,點D、E分別是邊AB、AC的中點,延長DE至F,使得AF//CD,連接BF、CF。求證:四邊形AFCD是菱形。
查看答案和解析>>
科目:初中數學 來源: 題型:
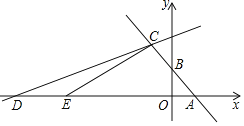
【題目】如圖,在平面直角坐標系中,函數y=﹣x+2的圖象與x軸,y軸分別交于點A,B,與函數y=![]() x+b的圖象交于點C(﹣2,m).
x+b的圖象交于點C(﹣2,m).
(1)求m和b的值;
(2)函數y=![]() x+b的圖象與x軸交于點D,點E從點D出發沿DA方向,以每秒2個單位長度勻速運動到點A(到A停止運動).設點E的運動時間為t秒.
x+b的圖象與x軸交于點D,點E從點D出發沿DA方向,以每秒2個單位長度勻速運動到點A(到A停止運動).設點E的運動時間為t秒.
①當△ACE的面積為12時,求t的值;
②在點E運動過程中,是否存在t的值,使△ACE為直角三角形?若存在,直接寫出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知頂點為(-3,-6)的拋物線![]() 經過點(-1,-4),下列結論中錯誤的是( )
經過點(-1,-4),下列結論中錯誤的是( )

A. ![]()
B. 若點(-2, ![]() ),(-5,
),(-5, ![]() ) 在拋物線上,則
) 在拋物線上,則![]()
C. ![]()
D. 關于![]() 的一元二次方程
的一元二次方程![]() 的兩根為-5和-1
的兩根為-5和-1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com