
如圖,在扇形OAB中,∠AOB=90°,半徑OA=6.將扇形OAB沿過(guò)點(diǎn)B的直線折疊。點(diǎn)O恰好落在弧AB上點(diǎn)D處,折痕交OA于點(diǎn)C,求整個(gè)陰影部分的周長(zhǎng)和面積。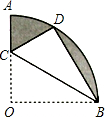
解:連接OD.
根據(jù)折疊的性質(zhì),CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等邊三角形,
∴∠DBO=60°,
∴∠CBO= ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OB•tan∠CBO=6× =
= ,
,
∴S△BDC=S△OBC= ×OB×OC=
×OB×OC= ×6×2
×6×2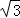 =6
=6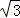 ,S扇形AOB=
,S扇形AOB=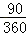 π×62=9π,
π×62=9π,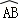 =
=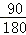 π×6=3π,
π×6=3π,
∴整個(gè)陰影部分的周長(zhǎng)為:AC+CD+BD+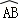 =AC+OC+OB+
=AC+OC+OB+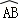 =OA+OB+
=OA+OB+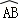 =6+6+3π=12+3π;
=6+6+3π=12+3π;
整個(gè)陰影部分的面積為:S扇形AOB﹣S△BDC﹣S△OBC=9π﹣6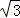 ﹣6
﹣6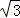 =9π﹣12
=9π﹣12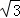 .
. 
解析試題分析:首先連接OD,由折疊的性質(zhì),可得CD=CO,BD=BO,∠DBC=∠OBC,則可得△OBD是等邊三角形,繼而求得OC的長(zhǎng),即可求得△OBC與△BCD的面積,又由在扇形OAB中,∠AOB=90°,半徑OA=6,即可求得扇形OAB的面積與 的長(zhǎng),繼而求得整個(gè)陰影部分的周長(zhǎng)和面積.
的長(zhǎng),繼而求得整個(gè)陰影部分的周長(zhǎng)和面積.
考點(diǎn):翻折變換(折疊問(wèn)題);等邊三角形的判定與性質(zhì);弧長(zhǎng)的計(jì)算;扇形面積的計(jì)算;解直角三角形.
點(diǎn)評(píng):此題考查了折疊的性質(zhì)、扇形面積公式、弧長(zhǎng)公式以及直角三角形的性質(zhì).此題難度適中,注意數(shù)形結(jié)合思想的應(yīng)用,注意輔助線的作法.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:單選題
已知兩圓半徑為5cm和3cm,圓心距為3cm,則兩圓的位置關(guān)系是( )
| A.相交 | B.內(nèi)含 | C.內(nèi)切 | D.外切 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:單選題
如圖,⊙O是△ABC的外接圓,若∠AOB=100°,則∠ACB的度數(shù)是( )
| A.40° | B.50° | C.60° | D.80° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分10分)如圖,AB是⊙O直徑,D為⊙O上一點(diǎn),AT平分∠BAD交⊙O于點(diǎn)T,過(guò)T作AD的垂線交AD的延長(zhǎng)線于點(diǎn)C.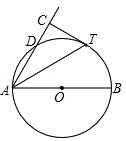
(1)求證:CT為⊙O的切線;
(2)若⊙O半徑為2,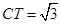 ,求AD的長(zhǎng).
,求AD的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
(10分)如圖,在△ABC中,AC=BC,AB是⊙C的切線,切點(diǎn)為D,直線AC交⊙C于點(diǎn)E、F,且CF= AC.
AC.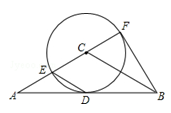
(1)求∠ACB的度數(shù);
(2)若AC=8,求△ABF的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省九年級(jí)上學(xué)期期中調(diào)研考試數(shù)學(xué)試卷(解析版) 題型:填空題
如圖,點(diǎn)A是反比例函數(shù)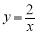 (
(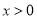 )的圖象上任意一點(diǎn),AB∥x軸交反比例函數(shù)
)的圖象上任意一點(diǎn),AB∥x軸交反比例函數(shù)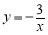 的圖象于點(diǎn)B,以AB為邊作
的圖象于點(diǎn)B,以AB為邊作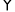 ABCD,其中C、D在x軸上,則
ABCD,其中C、D在x軸上,則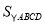 .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省九年級(jí)上學(xué)期期中考試數(shù)學(xué)試卷(解析版) 題型:選擇題
關(guān)于x的一元二次方程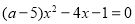 有實(shí)數(shù)根,則a滿足( )
有實(shí)數(shù)根,則a滿足( )
A.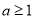 且
且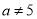 B.
B.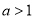 且
且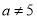 C.
C.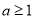 D.
D.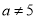
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com