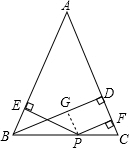
證明:過P作PG⊥BD于G,
∵BD⊥AC,PF⊥AC,
∴PG∥DF,GD∥PF(垂直于同一條直線的兩條直線互相平行),
∴四邊形PGDF是平行四邊形(兩條對邊互相平行的四邊形是平行四邊形);
又∠GDF=90°,
∴四邊形PGDF是矩形(有一個角是直角的平行四邊形是矩形),
∴PF=GD(矩形的對邊相等)①
∵四邊形PGDF是矩形
∴PG∥DF,即PG∥AC,
∴∠BPG=∠C(兩條直線平行,同位角相等),
又∵AB=AC(已知)
∴∠ABC=∠C(等腰三角形的兩底角相等),
∴∠BPG=∠ABC(等量代換)
∵∠PEB=∠BGP=90°(已證),BP=PB
∴△BPE≌△PBG(AAS)
∴PE=BG②
①+②:PE+PF=BG+GD
即PE+PF=BD.
分析:根據已知,過P作PG⊥BD于G,可得矩形PGDF,所以PF=GD①,再由矩形PGDF得PG∥AC,又由AB=AC得∠ABC=∠C,所以∠BPG=∠ABC,再∵∠PEB=∠BGP=90°,BP=PB,則△BPE≌△PBG,所以得
PE=BG②,①+②得出PE+PF=BD.
點評:此題考查的知識點是全等三角形的判定與性質及等腰三角形的性質,關鍵是作輔助線證矩形PGDF,再證△BPE≌△PBG.

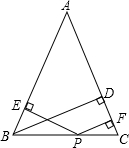 如圖,△ABC中,AB=AC,BD⊥AC于D,P是BC上任意一點,PE⊥AB于E,PF⊥AC于F.
如圖,△ABC中,AB=AC,BD⊥AC于D,P是BC上任意一點,PE⊥AB于E,PF⊥AC于F. 證明:過P作PG⊥BD于G,
證明:過P作PG⊥BD于G,

 已知,如圖,△ABC中,點D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如圖,△ABC中,點D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.