【答案】
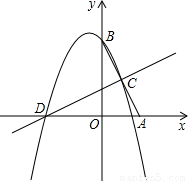
分析:(1)首先過C作CD⊥x軸于G.構造△OAB的中位線CG,根據A、B點的坐標及三角形中位線的性質不難求得點C的坐標.由于△ABO∽△ADC,利用相似三角形的性質解得AD的長,那么D點的坐標也就確定.
(2)運用待定系數法求解.假設過B(0,4),C(1,2),D(-3,0)的拋物線的關系式為y=ax
2+bx+c,將三點坐標值代入聯立組成三元一次方程組解得a、b、c的值.
(3)設點P的坐標為(x,y)連BD,過點P作PH⊥x軸于H,交BD于E.觀察圖象發現S
四邊形PBCD=S
△BCD+S
△PBD,
因為S
△BCD=S
△ACD為定值,所以要使四邊形PBCD的面積最大就是使△PBD的面積最大.再分別就①當P在BD間的拋物線上時(即-3<x<0);②當P在BC間的拋物線上時(即0<x<1)時,討論x的取值,進而得到P點的坐標,并驗證結果的合理性.
解答: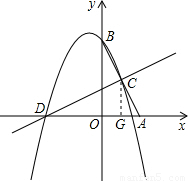
解:(1)過C作CD⊥x軸于G,
∵點C為線段AB的中點,
∴CG是△OAB的中位線,
∴點C的坐標是(1,2),┅┅┅┅┅┅┅┅(1分)
又∵OA=2,OB=4,
∴AB=

,AC=

,
顯然△ABO∽△ADC,
∴
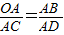
,
即
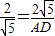
,┅┅┅┅┅┅┅┅┅┅┅(2分)
∴AD=5OD=AD-OA=3,
∴點D的坐標是(-3,0);┅┅┅┅┅┅┅┅┅(3分)
(2)解:設過B(0,4),C(1,2),D(-3,0)的拋物線的關系式為y=ax
2+bx+c,
∴
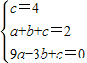
,┅┅┅┅┅┅(4分)
解得:
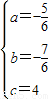
,┅┅┅┅┅┅┅┅┅┅┅┅(5分)
∴拋物線的關系式為
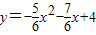
;┅┅┅┅┅┅┅┅┅(6分)
(3)解:設點P的坐標為(x,y)連BD,過點P作PH⊥x軸于H,交BD于E
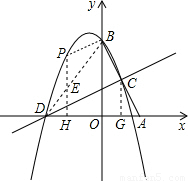
,
S
四邊形PBCD=S
△BCD+S
△PBD,
∵S
△BCD=S
△ACD為定值,
∴要使四邊形PBCD的面積最大就是使△PBD的面積最大,
①當P在BD間的拋物線上時,即-3<x<0,
S
△PBD=S
△PBE+S
△PED=

PE×DH+

PE×OH=

PE×OD=

PE,
∵PE=PH-EH=y
P-y
E,┅┅┅┅┅┅┅┅(7分)
直線BD的關系式為y=
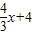
,

∴PE=
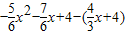
,
=
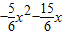
,
當x=
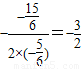
時,PE最大為
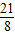
,
∴點P的坐標(
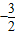
,
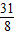
),┅┅┅┅┅┅┅┅┅┅(8分)
②當P在BC間的拋物線上時,即0<x<1,
同理可求出四邊形PBCD的面積,
很顯然,此時四邊形PBCD的面積要小于點P在BD間的拋物線上時的四邊形PBCD的面積,
故P點的坐標是(
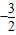
,
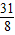
).┅┅┅┅┅┅┅┅┅(9分)
點評:本題是二次函數的綜合題型,其中涉及到的知識點有利用待定系數法求拋物線的解析式和三角形的面積求法.在求有關動點問題時要注意分析題意分情況討論結果;并有效利用了坐標與線段的數形結合.

 解:(1)過C作CD⊥x軸于G,
解:(1)過C作CD⊥x軸于G, ,AC=
,AC= ,
,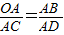 ,
,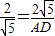 ,┅┅┅┅┅┅┅┅┅┅┅(2分)
,┅┅┅┅┅┅┅┅┅┅┅(2分)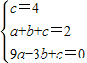 ,┅┅┅┅┅┅(4分)
,┅┅┅┅┅┅(4分)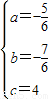 ,┅┅┅┅┅┅┅┅┅┅┅┅(5分)
,┅┅┅┅┅┅┅┅┅┅┅┅(5分)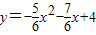 ;┅┅┅┅┅┅┅┅┅(6分)
;┅┅┅┅┅┅┅┅┅(6分) ,
, PE×DH+
PE×DH+ PE×OH=
PE×OH= PE×OD=
PE×OD= PE,
PE,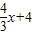 ,
,
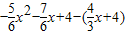 ,
,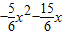 ,
,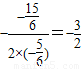 時,PE最大為
時,PE最大為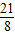 ,
,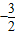 ,
,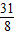 ),┅┅┅┅┅┅┅┅┅┅(8分)
),┅┅┅┅┅┅┅┅┅┅(8分)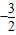 ,
,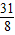 ).┅┅┅┅┅┅┅┅┅(9分)
).┅┅┅┅┅┅┅┅┅(9分)

 名校課堂系列答案
名校課堂系列答案
 如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′.
如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′.

 ,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件:
,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件: