
【題目】如圖,已知∠DAC=90°,△ABC是等邊三角形,點P為射線AD上任意一點(點P與點A不重合),連結CP,將線段CP繞點C順時針旋轉60°得到線段CQ,連結QB并延長交直線AD于點E.
(1)如圖,求∠QEP的度數;
(2)如圖,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的長.

【答案】(1)60°,理由見解析;(2)BQ=2![]() ﹣2
﹣2![]() .
.
【解析】
(1)先證明出△CQB≌△CPA,即可得出∠QEP=60°;
(2)作CH⊥AD于H,如圖2,證明△ACP≌△BCQ,則AP=BQ,由∠DAC=135°,∠ACP=15°,得出AH=3,CH=3![]() ,即可得出PH=CH=3
,即可得出PH=CH=3![]() ,即可得出結論.
,即可得出結論.
(1)如圖1,∵PC=CQ,且∠PCQ=60°,則△CQB和△CPA中,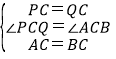 ,∴△CQB≌△CPA(SAS),
,∴△CQB≌△CPA(SAS),
∴∠CQB=∠CPA,又因為△PEM和△CQM中,∠EMP=∠CMQ, ∴∠QEP=∠QCP=60°.
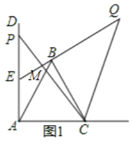
(2)作CH⊥AD于H,如圖2,
∵△ABC是等邊三角形,
∴AC=BC,∠ACB=60°,
∵線段CP繞點C順時針旋轉60°得到線段CQ,
∴CP=CQ,∠PCQ=6O°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
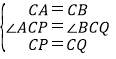
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,∴∠APC=30°,∠PCB=45°,∴△ACH為等腰直角三角形,
∴AH=CH=![]() AC=
AC=![]() ×4=2
×4=2![]() ,在Rt△PHC中,PH=
,在Rt△PHC中,PH=![]() CH=2
CH=2![]() ,∴PA=PH﹣AH=2
,∴PA=PH﹣AH=2![]() ﹣2
﹣2![]() ,
,
∴BQ=2![]() ﹣2
﹣2![]() .
.



 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:初中數學 來源: 題型:
【題目】小明家的洗手盆上裝有一種抬啟式水龍頭(如圖1),完全開啟后,水流路線呈拋物線,把手端點A,出水口B和落水點C恰好在同一直線上,點A至出水管BD的距離為12cm,洗手盆及水龍頭的相關數據如圖2所示,現用高10.2cm的圓柱型水杯去接水,若水流所在拋物線經過點D和杯子上底面中心E,則點E到洗手盆內側的距離EH為_________cm.

(第16題圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 為鼓勵創業,某市政府制定了小型企業的優惠政策,許多小型企業應運而生,某社區統計了該社區今年1~6月份新注冊小型企業的數量,并將結果繪制成如下的條形統計圖和扇形統計圖:
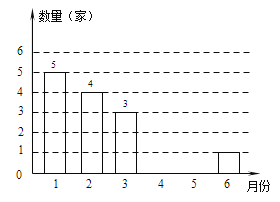

根據以上信息解答下列問題:
(1)該社區1~6月新注冊小型企業一共有__________家;
(2)補全條形統計圖。
(3)扇形統計圖中“4月份”所在扇形的圓心角的度數為 ;
(4)如果該市今年1~6月份新注冊小型企業共有1200家,估計全市今年1月份新注冊小型企業的數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我區積極開展“體育大課間”活動,引導學生堅持體育鍛煉,某校根據實際情況,決定主要開設A:乒乓球,B:籃球,C:跑步.D:足球四種運動項目.為了解學生最喜歡哪一種項目,隨機抽取了部分學生進行調査,并將調查結果繪制成如下統計圖.請你結合圖中信息解答下列問題:
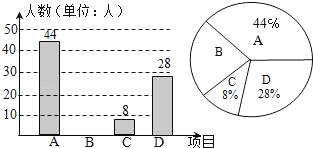
(1)求樣本中最喜歡B項目的人數百分比和其所在扇形圖中的圓心角的度數;
(2)請把條形統計圖補充完整;
(3)己知該校有2000人,請根據樣本估計全校最喜歡足球的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有50個房間供游客居住,當每個房間定價120元時,房間會全部住滿,當每個房間每天的定價每增加10元時,就會有一個房間空閑。如果游客居住房間,賓館需對每個房間每天支出20元的各種費用,設每個房間定價增加10 x元(x為整數)。
(1)(2分)直接寫出每天游客居住的房間數量y與x的函數關系式。
(2)(4分)設賓館每天的利潤為W元,當每間房價定價為多少元時,賓館每天所獲利潤最大,最大利潤是多少?
(3)(4分)某日,賓館了解當天的住宿的情況,得到以下信息:①當日所獲利潤不低于5000元,②賓館為游客居住的房間共支出費用沒有超過600元,③每個房間剛好住滿2人。問:這天賓館入住的游客人數最少有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個幾何體由大小相同的正方體搭成,從上面看到的幾何體的形的形狀狀圖如圖所示,其中小正方形中的數字表示在該位置的小正方體的個數,

(1)請畫出從正面和左面看到的這個幾何體的形狀圖.
(2)若每個小正方圖的棱長都為1,則搭成的這個幾何體的體積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:b是最小的正整數,且a、b滿足(c﹣5)2+|a+b|=0.
![]()
(1)請求出a、b、c的值;
(2)a、b、c所對應的點分別為A、B、C,點P為一動點,其對應的數為x,點P在0到2之間運動時(即0≤x≤2時),請化簡式子:|x+1|-|x-1|+2|x+5|(請寫出化簡過程)
(3)在(1)(2)的條件下,點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和5個單位長度的速度向右運動,假設t秒鐘過后,若點B與點C之間的距離表示為BC,點A與點B之間的距離表示為AB.請問:BC-AB的值是否隨著時間t的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在RtΔABC中,∠C=90°,∠ABC=30°,AB=8,將△ABC沿CB方向向右平移得到△DEF.若四邊形ABED的面積為8,則平移距離為__.
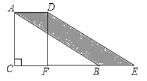
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠生產的某種產品按質量分為10個檔次,第1檔次(最低檔次)的產品一天能生產95件,每件利潤6元.每提高一個檔次,每件利潤增加2元,但一天產量減少5件.
(1)若生產第![]() 檔次的產品一天的總利潤為
檔次的產品一天的總利潤為![]() 元(其中
元(其中![]() 為正整數,且1≤
為正整數,且1≤![]() ≤10),求出
≤10),求出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)若生產第x檔次的產品一天的總利潤為1120元,求該產品的質量檔次.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com