
如圖,有長為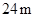 的籬笆,現一面利用墻(墻的最大可用長度
的籬笆,現一面利用墻(墻的最大可用長度 為
為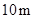 )圍成中間隔有一道籬笆的長方形花圃,設花圃的寬
)圍成中間隔有一道籬笆的長方形花圃,設花圃的寬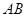 為
為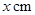 ,面積為
,面積為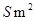 .
.
(1)求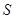 與
與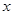 的函數關系式.
的函數關系式.
(2)要圍成面積為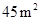 的花圃,
的花圃,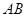 的長是多少米?
的長是多少米?
(3)能圍成面積比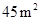 還大的花圃嗎?如果能,求出最大面積,并說明圍法;如果不能,請說明理由.
還大的花圃嗎?如果能,求出最大面積,并說明圍法;如果不能,請說明理由.

(1)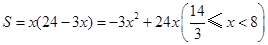 ;(2)
;(2)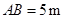 ;
;
(3)長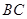 為
為 ,寬為
,寬為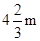 .這時花圃面積最大,為
.這時花圃面積最大,為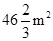 .
.
【解析】
試題分析:(1)現年表示出BC的長,再根據矩形面積公式即得函數關系式;
(2)把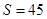 代入(1)中的函數關系式,即可求得結果,注意對所求值的取舍;
代入(1)中的函數關系式,即可求得結果,注意對所求值的取舍;
(3)求出(1)中的函數的最大值即可。
(1)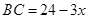 ,故
,故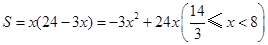 .
.
(2)由已知得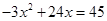 ,即
,即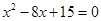 ,解得
,解得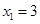 ,
,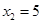 ,
,
當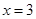 時,
時,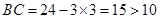 ,不合題意,故
,不合題意,故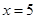 ,即
,即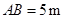 .
.
(3)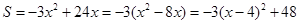 .
.
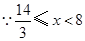 ,
,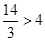 ,
,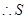 隨著
隨著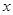 的增大而減小.
的增大而減小.
故當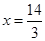 時,
時,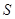 有最大值
有最大值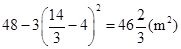 .
.
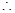 能圍成面積比
能圍成面積比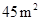 還大的花圃.
還大的花圃.
圍法: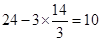 ,花圃的長
,花圃的長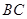 為
為 ,寬為
,寬為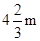 .這時花圃面積最大,為
.這時花圃面積最大,為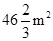 .
.
考點:本題考查的是二次函數的應用
點評:解答本題的關鍵是運用長方形面積計算方法列一元二次方程解決實際問題與根的判別式的應用.


科目:初中數學 來源: 題型:
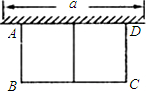 如圖,有長為24m的籬笆,一面利用墻(墻的最大可用長度a為10m)圍成中間隔有一道籬笆的長方形花輔,設花圃的寬AB為x(m),面積為y(m2),求:
如圖,有長為24m的籬笆,一面利用墻(墻的最大可用長度a為10m)圍成中間隔有一道籬笆的長方形花輔,設花圃的寬AB為x(m),面積為y(m2),求:查看答案和解析>>
科目:初中數學 來源: 題型:
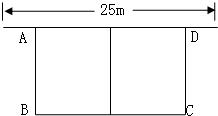 24、如圖,有長為48米的籬笆,一面利用墻(墻的最大可用長度25米),圍成中間隔有一道籬笆的長方形花圃ABCD.
24、如圖,有長為48米的籬笆,一面利用墻(墻的最大可用長度25米),圍成中間隔有一道籬笆的長方形花圃ABCD.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,有長為24的籬笆,圍成矩形花圃,且花圃的長可借用一段墻體(墻體的最大可用長度是10米),求圍成的花圃面積y與AB的長x的函數關系,并確定y的最大值.
如圖,有長為24的籬笆,圍成矩形花圃,且花圃的長可借用一段墻體(墻體的最大可用長度是10米),求圍成的花圃面積y與AB的長x的函數關系,并確定y的最大值.查看答案和解析>>
科目:初中數學 來源: 題型:
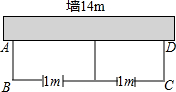 如圖,有長為22米的籬笆,一面利用墻(墻的最大可用長度為14米),圍成中間隔有一道籬笆的長方形花圃,為了方便出入,在建造籬笆花圃時,在BC上用其他材料造了寬為1米的兩個小門,此時花圃的面積剛好為45米2,求此時花圃的長和寬.
如圖,有長為22米的籬笆,一面利用墻(墻的最大可用長度為14米),圍成中間隔有一道籬笆的長方形花圃,為了方便出入,在建造籬笆花圃時,在BC上用其他材料造了寬為1米的兩個小門,此時花圃的面積剛好為45米2,求此時花圃的長和寬.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com