【題目】如圖，在平面直角坐標系xOy中，過坐標原點O的直線l與雙曲線y= 
相交于點A（m，3）． 
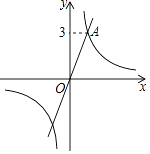
（1）求直線l的表達式；
（2）過動點P（n，0）且垂于x軸的直線與l及雙曲線的交點分別為B，C，當點B位于點C上方時，寫出n的取值范圍 ．
孟建平小學滾動測試系列答案科目：初中數學 來源： 題型：
【題目】某廠工人小王某月工作的部分信息如下：
信息一：工作時間：每天上午8：00～12：00，下午14：00～18：00，每月25天；
信息二：生產甲、乙兩種產品，并且按規定每月生產甲產品的件數不少于45件.
生產產品件數與所用時間之間的關系見下表：
生產甲產品件數（件） | 生產乙產品件數（件） | 所用總時間（分） |
10 | 10 | 500 |
15 | 20 | 900 |
信息三：按件計酬，每生產一件甲產品可得6元，每生產一件乙產品可得10元.
根據以上信息，回答下列問題：
(1)小王每生產一件甲種產品，每生產一件乙種產品分別需要多少分？
(2)小王該月最多能得多少元？此時生產甲、乙兩種產品分別多少件？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】△ABC中，AB=AC，∠A=30°，以B為圓心，BC長為半徑畫弧，分別交AC，AB于D，E兩點，并連結BD，DE． 則∠BDE的度數為 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，一次函數 
與反比例函數 
的圖象在第一象限的交點為A（1，n）． 
（1）求m與n的值；
（2）設一次函數的圖象與x軸交于點B，連結OA，求∠BAO的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，線段AC和直線l分別垂直線段AB于點A，B．點P是線段AB上的一個動點，由A移動到B，連接CP，過點P作PD⊥CP交l于點D，設線段AP的長為x，BD的長為y，在下列圖象中，能大致表示y與x之間函數關系的是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】太陽影子定位技術是通過分析視頻中物體的太陽影子變化，確定視頻拍攝地點的一種方法．為了確定視頻拍攝地的經度，我們需要對比視頻中影子最短的時刻與同一天東經120度影子最短的時刻．在一定條件下，直桿的太陽影子長度l（單位：米）與時刻t（單位：時）的關系滿足函數關系l=at2+bt+c（a，b，c是常數），如圖記錄了三個時刻的數據，根據上述函數模型和記錄的數據，則該地影子最短時，最接近的時刻t是（ ）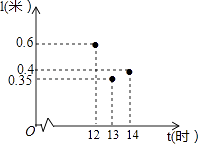 
A.12.75
B.13
C.13.33
D.13.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=BC，以AB為直徑的⊙O分別交AC，BC于點D，E，過點A作⊙O的切線交BC的延長線于點F，連接AE． 
（1）求證：∠ABC=2∠CAF；
（2）過點C作CM⊥AF于M點，若CM=4，BE=6，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是拋物線y1=ax2+bx+c（a≠0）圖象的一部分，拋物線的頂點坐標A（1，3），與x軸的一個交點B（4，0），直線y2=mx+n（m≠0）與拋物線交于A，B兩點，下列結論： ①2a+b=0；②abc＞0；③方程ax2+bx+c=3有兩個相等的實數根；④拋物線與x軸的另一個交點是（﹣1，0）；⑤當1＜x＜4時，有y2＜y1 ，
其中正確的是 ．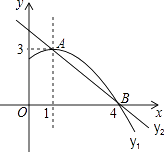 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點B、E、C、F在一條直線上，AB=DF，AC=DF，BE=FC． 
（1）求證：△ABC≌△DFE；
（2）連接AF、BD，求證：四邊形ABDF是平行四邊形．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
