
【題目】已知關于x的一元二次方程x2+(2x+1)x+k2=0①有兩個不相等的實數根.
(1)求k的取值范圍;
(2)設方程①的兩個實數根分別為x1 , x2 , 當k=1時,求x12+x22的值.
【答案】
(1)解:∵方程有兩個不相等的實數根,
∴△=(2k+1)2﹣4k2=4k+1>0,
解得:k>﹣ ![]() ;
;
(2)解:當k=1時,方程為x2+3x+1=0,
∵x1+x2=﹣3,x1x2=1,
∴x12+x22=(x1+x2)2﹣2x1x2=9﹣2=7.
【解析】(1)由方程有兩個不相等的實數根知△>0,列不等式求解可得;(2)將k=1代入方程,由韋達定理得出x1+x2=﹣3,x1x2=1,代入到x12+x22=(x1+x2)2﹣2x1x2可得.
【考點精析】本題主要考查了求根公式和根與系數的關系的相關知識點,需要掌握根的判別式△=b2-4ac,這里可以分為3種情況:1、當△>0時,一元二次方程有2個不相等的實數根2、當△=0時,一元二次方程有2個相同的實數根3、當△<0時,一元二次方程沒有實數根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商才能正確解答此題.


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2+bx+c的圖象經過點A(m,0)、B(0,n),其中m、n是方程x2﹣6x+5=0的兩個實數根,且m<n.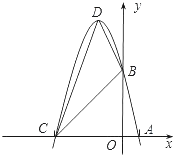
(1)求拋物線的解析式;
(2)設(1)中的拋物線與x軸的另一個交點為C,拋物線的頂點為D,求C、D點的坐標和△BCD的面積;
(3)P是線段OC上一點,過點P作PH⊥x軸,交拋物線于點H,若直線BC把△PCH分成面積相等的兩部分,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某跳水隊為了解運動員的年齡情況,作了一次年齡調查,根據跳水運動員的年齡(單位:歲),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
(1)本次接受調查的跳水運動員人數為 , 圖①中m的值為;
(2)求統計的這組跳水運動員年齡數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠C=90°,點M從點C出發沿CB方向以1cm/s的速度勻速運動,到達點B停止運動,在點M的運動過程中,過點M作直線MN交AC于點N,且保持∠NMC=45°,再過點N作AC的垂線交AB于點F,連接MF,將△MNF關于直線NF對稱后得到△ENF,已知AC=8cm,BC=4cm,設點M運動時間為t(s),△ENF與△ANF重疊部分的面積為y(cm2).
(1)在點M的運動過程中,能否使得四邊形MNEF為正方形?如果能,求出相應的t值;如果不能,說明理由;
(2)求y關于t的函數解析式及相應t的取值范圍;
(3)當y取最大值時,求sin∠NEF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,菱形ABCD中,AB=5cm,動點P從點B出發,沿折線BC﹣CD﹣DA運動到點A停止,動點Q從點A出發,沿線段AB運動到點B停止,它們運動的速度相同,設點P出發xs時,△BPQ的面積為ycm2 , 已知y與x之間的函數關系如圖②所示,其中OM,MN為線段,曲線NK為拋物線的一部分,請根據圖中的信息,解答下列問題: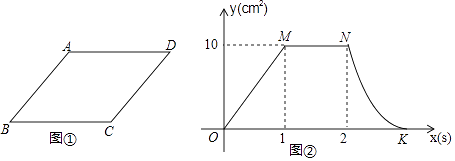
(1)當1<x<2時,△BPQ的面積(填“變”或“不變”);
(2)分別求出線段OM,曲線NK所對應的函數表達式;
(3)當x為何值時,△BPQ的面積是5cm2?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在黃岡長江大橋的東端一處空地上,有一塊矩形的標語牌ABCD(如圖所示),已知標語牌的高AB=5m,在地面的點E處,測得標語牌點A的仰角為30°,在地面的點F處,測得標語牌點A的仰角為75°,且點E,F,B,C在同一直線上,求點E與點F之間的距離.(計算結果精確到0.1米,參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)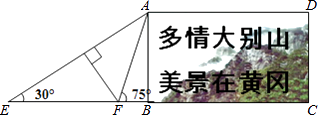
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=α(90°<α<180°),將△ABC繞著點A逆時針旋轉2β(0°<β<90°)后得△AED,其中點E、D分別和點B、C對應,聯結CD,如果CD⊥ED,請寫出一個關于α與β的等量關系的式子 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ![]() ,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連接EF,則線段EF長度的最小值為 .
,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連接EF,則線段EF長度的最小值為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣x+4的圖象與反比例y= ![]() (k為常數,且k≠0)的圖象交于A(1,a),B兩點.
(k為常數,且k≠0)的圖象交于A(1,a),B兩點. 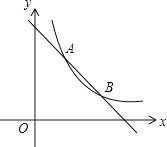
(1)求反比例函數的表達式及點B的坐標;
(2)在x軸上找一點P,使PA+PB的值最小,求PA+PB的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com