
【題目】某工廠計劃生產![]() 兩種產品共60件,需購買甲、乙兩種材料.生產一件
兩種產品共60件,需購買甲、乙兩種材料.生產一件![]() 產品需甲種材料4千克;生產一件
產品需甲種材料4千克;生產一件![]() 產品需甲、乙兩種材料各3千克.經測算,購買甲、乙兩種材料各1千克共需資金60元;購買甲種材料2千克和乙種材料3千克共需資金155元.
產品需甲、乙兩種材料各3千克.經測算,購買甲、乙兩種材料各1千克共需資金60元;購買甲種材料2千克和乙種材料3千克共需資金155元.
(1)甲、乙兩種材料每千克分別是多少元?
(2)現工廠用于購買甲、乙兩種材料的資金不超過9900元,且生產![]() 產品不少于38件,問符合生產條件的生產方案有哪幾種?
產品不少于38件,問符合生產條件的生產方案有哪幾種?
(3)在(2)的條件下,若生產一件![]() 產品需加工費40元,生產一件
產品需加工費40元,生產一件![]() 產品需加工費50元,應選擇哪種生產方案,使生產這60件產品的成本最低(成本=材料費+加工費)?
產品需加工費50元,應選擇哪種生產方案,使生產這60件產品的成本最低(成本=材料費+加工費)?
【答案】(1) 甲種材料每千克25元,乙種材料每千克35元;(2) 有三種方案;(3) 生產![]() 產品22件,
產品22件,![]() 產品38件成本最低
產品38件成本最低
【解析】
(1)設甲材料每千克x元,乙材料每千克y元,根據購買甲、乙兩種材料各1千克共需資金60元;購買甲種材料2千克和乙種材料3千克共需資金155元,可列出方程組
![]() ,解方程組即可得到甲材料每千克25元,乙材料每千克35元;
,解方程組即可得到甲材料每千克25元,乙材料每千克35元;
(2)設生產A產品m件,生產B產品(60-m)件,先表示出生產這60件產品的材料費為25×4m+35×1m+25×3(60-m)+35×3(60-m)=-45m+10800,根據購買甲、乙兩種材料的資金不超過9900元得到-45m+10800≤9900,根據生產B產品不少于38件得到60-m≥38,然后解兩個不等式求出其公共部分得到20≤m≤22,而m為整數,則m的值為20,21,22,易得符合條件的生產方案;
(3)設總生產成本為W元,加工費為:40m+50(60-m),根據成本=材料費+加工費得到W=-45m+10800+40m+50(60-m)=-55m+13800,根據一次函數的性質得到W隨m的增大而減小,然后把m=22代入,即可得到最低成本的生產方案.
(1)設甲種材料每千克![]() 元,乙種材料每千克
元,乙種材料每千克![]() 元,依題意得:
元,依題意得:
![]() 解得
解得![]()
答:甲種材料每千克25元,乙種材料每千克35元.
(2)生產![]() 產品
產品![]() 件,生產
件,生產![]() 產品
產品![]() 件.依題意得:
件.依題意得:
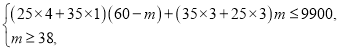
解得![]() .
.
![]()
![]() 的值為整數,
的值為整數,
![]() 的值為38,39,40.
的值為38,39,40.
![]() 共有三種方案:
共有三種方案:
| 22 | 21 | 20 |
| 38 | 39 | 40 |
(3)設生產成本為![]() 元,則
元,則
![]() ,
,
![]() ,
,![]() 隨
隨![]() 的增大而增大.
的增大而增大.
![]() 當
當![]() 時,總成本最低.
時,總成本最低.
答:生產![]() 產品22件,
產品22件,![]() 產品38件成本最低.
產品38件成本最低.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,已知四邊形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD為銳角.
(1)求證:AD⊥BF;
(2)若BF=BC,求∠ADC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解放中學為了了解學生對新聞、體育、動畫、娛樂四類電視節目的喜愛程度,隨機抽取了部分學生進行調查(每人限選1項),現將調查結果繪制成如下兩幅不完整的統計圖,根據圖中所給的信息解答下列問題.
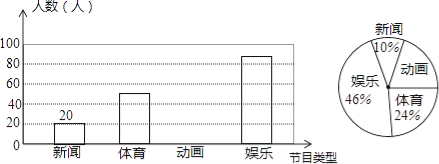
(1)喜愛動畫的學生人數和所占比例分別是多少?
(2)請將條形統計圖補充完整;
(3)若該校共有學生1000人,依據以上圖表估計該校喜歡體育的人數約為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
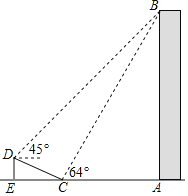
【題目】如圖,在大樓AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高為DE,在斜坡下的點C處測得樓頂B的仰角為64°,在斜坡上的點D處測得樓頂B的仰角為45°,其中A、C、E在同一直線上.
,高為DE,在斜坡下的點C處測得樓頂B的仰角為64°,在斜坡上的點D處測得樓頂B的仰角為45°,其中A、C、E在同一直線上.
(1)求斜坡CD的高度DE;
(2)求大樓AB的高度;(參考數據:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中數學 來源: 題型:
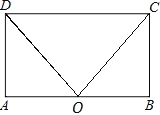
【題目】如圖,在平行四邊形ABCD中,點O是AB的中點,且OC=OD.
(1)求證:平行四邊形ABCD是矩形;
(2)若AD=3,∠COD=60°,求矩形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(﹣1,0),與y軸的交點B在(0,﹣2)和(0,﹣1)之間(不包括這兩點),對稱軸為直線x=1.下列結論:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正確結論的選項是( )
⑤b>c.其中含所有正確結論的選項是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,平行四邊形ABCD和平行四邊形CDEF有公共邊CD,邊AB和EF在同一條直線上,AC⊥CD且AC=AF,過點A作AH⊥BC交CF于點G,交BC于點H,連接EG.
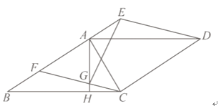
(1)若AE=2,CD=5,則△BCF的面積為 ;△BCF的周長為 ;
(2)求證:BC=AG+EG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A,B兩點在數軸上,點A在原點O的左邊,表示的數為﹣10,點B在原點的右邊,且BO=3AO.點M以每秒3個單位長度的速度從點A出發向右運動.點N以每秒2個單位長度的速度從點O出發向右運動(點M,點N同時出發).
(1)數軸上點B對應的數是 ,點B到點A的距離是 ;
(2)經過幾秒,原點O是線段MN的中點?
(3)經過幾秒,點M,N分別到點B的距離相等?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著我國經濟社會的發展,人民對于美好生活的追求越來越高,某社區為了了解家庭對于文化教育的消費情況,隨機抽取部分家庭,對每戶家庭的文化教育年消費金額進行問卷調查,根據調查結果繪制成如下兩幅不完整的統計圖表.
級別 | 家庭的文化教育消費金額 | 戶數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
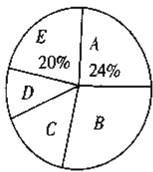
請你根據統計圖表提供的信息,解答下列問題:
(1)本次被調查的家庭有___________戶,表中![]() ___________;
___________;
(2)在扇形統計圖中,![]() 組所在扇形的圓心角為多少度?
組所在扇形的圓心角為多少度?
(3)這個社區有![]() 戶家庭,請你估計年文化教育消費在
戶家庭,請你估計年文化教育消費在![]() 元以上的家庭有多少戶.
元以上的家庭有多少戶.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com