
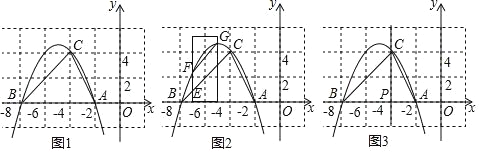
【題目】如圖1,拋物線y=﹣![]() x2+bx+c經過點A(﹣2,0),B(﹣8,0),C(﹣4,4).
x2+bx+c經過點A(﹣2,0),B(﹣8,0),C(﹣4,4).
(1)求這個拋物線的表達式;
(2)如圖2,一把寬為2的直尺的右邊緣靠在直線x=﹣4上,當直尺向左平移過程中刻度線0始終在x軸上,直尺的右邊邊緣與拋物線和直線BC分別交于G、D點,直尺的左邊邊緣與拋物線和直線BC分別交于F、E點,當圖中四邊形DEFG是平行四邊形時,此時直尺左邊邊緣與直線BC的交點E的刻度是多少?
(3)如圖3,在直線x=﹣4上找一點K,使得∠ACP+∠AKC=∠ABC(直線x=﹣4與x軸交于P點),請直接寫出K點的坐標.
【答案】(1)y=![]() x2-5x-8,
x2-5x-8,
(2)E(-7,1)
(3)K(-4,6)或(-4,-6).
【解析】
(1)將A(-2,0),B(-8,0)代入函數解析式即可求解,
(2)根據圖像性質求出直線BC的解析式為y=x+8,設D(a,a+8),再表示出G(a,![]() a2-5a-8),E(a-2,a+6), F(a-2,
a2-5a-8),E(a-2,a+6), F(a-2,![]() a2-3a),根據DG=EF即可解題,
a2-3a),根據DG=EF即可解題,
(3)根據網格點特征,即可求出K的坐標.
解:(1)將點A(-2,0),B(-8,0)代入y=![]() x2+bx+c中得:b=-5,c=-8,
x2+bx+c中得:b=-5,c=-8,
∴拋物線的解析式是y=![]() x2-5x-8,
x2-5x-8,
(2)如下圖,
∵A(-2,0),B(-8,0),C(-4,4),
∴直線BC的解析式為y=x+8,
根據題意可知∠ABC=45°,
∴設D(a,a+8),則G(a,![]() a2-5a-8),
a2-5a-8),
E(a-2,a+6),則F(a-2,![]() a2-3a),
a2-3a),
∵四邊形ABCD是平行四邊形,
∴DG=EF即![]() a2-5a-8-(a+8)=
a2-5a-8-(a+8)=![]() a2-3a-(a+6),
a2-3a-(a+6),
解得:a=-5,
∴E(-7,1)

(3)由題可知∠ABC=45°,即在直線x=-4上找一點K,使得∠ACP+∠AKC=45°,
根據網格的特征即可找到點K(-4,6)或(-4,-6).


科目:初中數學 來源: 題型:
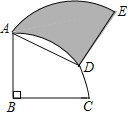
【題目】如圖,將半徑為4,圓心角為90°的扇形BAC繞A點逆時針旋轉60°,點B、C的對應點分別為點D、E且點D剛好在![]() 上,則陰影部分的面積為_____.
上,則陰影部分的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】校體育組為了解全校學生“最喜歡的一項球類項目”,隨機抽取了部分學生進行調查,下面是根據調查結果繪制的不完整的統計圖:

請你根據統計圖回答下列問題:
(1)喜歡乒乓球的學生所占的百分比是多少?并請補全條形統計圖;
(2)請你估計全校500名學生中最喜歡“排球”項目的有多少名?
(3)在扇形統計圖中,“籃球”部分所對應的圓心角是多少度?
(4)籃球教練在制定訓練計劃前,將從最喜歡籃球項目的甲、乙、丙、丁四名同學中任選兩人進行個別座談,請用列表法或樹狀圖法求抽取的兩人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,AB=8,點P在邊CD上,tan∠PBC=![]() ,點Q是在射線BP上的一個動點,過點Q作AB的平行線交射線AD于點M,點R在射線AD上,使RQ始終與直線BP垂直.
,點Q是在射線BP上的一個動點,過點Q作AB的平行線交射線AD于點M,點R在射線AD上,使RQ始終與直線BP垂直.
(1)如圖1,當點R與點D重合時,求PQ的長;
(2)如圖2,試探索: ![]() 的比值是否隨點Q的運動而發生變化?若有變化,請說明你的理由;若沒有變化,請求出它的比值;
的比值是否隨點Q的運動而發生變化?若有變化,請說明你的理由;若沒有變化,請求出它的比值;
(3)如圖3,若點Q在線段BP上,設PQ=x,RM=y,求y關于x的函數關系式,并寫出它的定義域.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在等邊三角形ABC中,BC=8cm,射線AG∥BC,點E從點A出發沿射線AG以1cm/s的速度運動,同時點F從點B出發沿射線BC以2cm/s的速度運動,設運動時間為t(s).
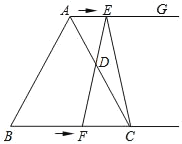
(1)連接EF,當EF經過AC邊的中點D時,求證:四邊形AFCE是平行四邊形;
(2)填空:①當t為 s時,四邊形ACFE是菱形;②當t為 s時,△ACE的面積是△ACF的面積的2倍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了推進球類運動的發展,某校組織校內球類運動會,分籃球、足球、排球、羽毛球、乒乓球五項,要求每位學生必須參加一項并且只能參加一項,某班有一名學生根據自己了解的班內情況繪制了如圖所示的不完整統計表和扇形統計圖.

請根據圖表中提供的信息,解答下列問題:
(1)圖表中m=________,n=________;
(2)若該校學生共有1000人,則該校參加羽毛球活動的人數約為________人;
(3)該班參加乒乓球活動的4位同學中,有3位男同學(分別用A,B,C表示)和1位女同學(用D表示),現準備從中選出兩名同學參加雙打比賽,用樹狀圖或列表法求出恰好選出一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
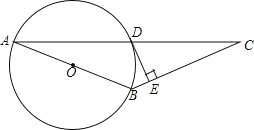
【題目】已知:如圖,AB為⊙O的直徑,⊙O過AC的中點D,DE⊥BC于點E.
(1)求證:DE為⊙O的切線;
(2)若DE=2,tanC=![]() ,求⊙O的直徑.
,求⊙O的直徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,∠ABC=90°,∠C=30°,AC 的垂直平分線交 BC 于點 D,交AC 于點 E.
(1)判斷 BE 與△DCE 的外接圓⊙O 的位置關系,并說明理由;
(2)若 BE=![]() ,BD=1,求△DCE 的外接圓⊙O 的直徑.
,BD=1,求△DCE 的外接圓⊙O 的直徑.
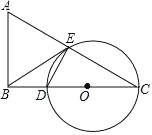
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣![]() x2+
x2+![]() x﹣1與x軸交于點A,B(點A在點B的左側),與y軸交于點C,其頂點為D.將拋物線位于直線l:y=t(t<
x﹣1與x軸交于點A,B(點A在點B的左側),與y軸交于點C,其頂點為D.將拋物線位于直線l:y=t(t<![]() )上方的部分沿直線l向下翻折,拋物線剩余部分與翻折后所得圖形組成一個“M”形的新圖象.
)上方的部分沿直線l向下翻折,拋物線剩余部分與翻折后所得圖形組成一個“M”形的新圖象.
(1)點A,B,D的坐標分別為 , , ;
(2)如圖①,拋物線翻折后,點D落在點E處.當點E在△ABC內(含邊界)時,求t的取值范圍;
(3)如圖②,當t=0時,若Q是“M”形新圖象上一動點,是否存在以CQ為直徑的圓與x軸相切于點P?若存在,求出點P的坐標;若不存在,請說明理由.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/28/2213337932849152/2214008649842688/STEM/890e59b444e5404588b8511540e03e41.png]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com