
在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直線為x軸和y軸,建立如圖所示的平面直角坐標系.F是BC上的一個動點(不與B、C重合),過F點的反比例函數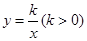 的圖象與AC邊交于點E.
的圖象與AC邊交于點E.
(1)求證:AE•AO=BF•BO;
(2)若點E的坐標為(2,4),求經過O、E、F三點的拋物線的解析式;
(3)是否存在這樣的點F,使得將△CEF沿EF對折后,C點恰好落在OB上?若存在,求出此時的OF的長:若不存在,請說明理由.
證明:(1)∵E,F點都在反比例函數圖象上,
∴根據反比例函數的性質得出,![]() ,
,
∴AE•AO=BF•BO;
(2)∵點E的坐標為(2,4),
∴AE•AO=BF•BO=8,
∵BO=6,∴BF=![]() ,
,
∴F(6,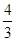 ),
),
分別代入二次函數解析式得: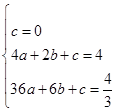 ,
,
解得: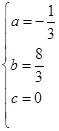 ,
,
∴![]() ;
;
(3)如果設折疊之后C點在OB上的對稱點為C',連接C'E、C'F,過E作EG垂直于OB于點G,則根據折疊性質、相似三角形、勾股定理有以下幾個關系可以考慮:
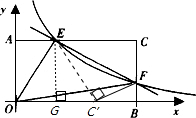 設BC'=a,BF=b,則C'F=CF=
設BC'=a,BF=b,則C'F=CF=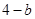 .
.
∴點的坐標F(6,b),E(1.5b,4).
EC'=EC=![]() ,
,
∴在Rt△C'BF中,![]() ①
①
∵Rt△EGC'與∽Rt△C'BF,
∴(![]() ):(
):(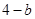 )=4:a=(
)=4:a=(![]() ):b ②,
):b ②,
解得:![]() ,
,
∴F點的坐標為(6,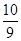 ).
).
∴FO= 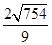 .
.
解析:略


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優沖刺100分系列答案
全優沖刺100分系列答案科目:初中數學 來源: 題型:
| k | x |
 存在,求出點F的坐標;若不存在,請說明理由.
存在,求出點F的坐標;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示的平面直角坐標系.F是邊BC上的一個動點(不與B,C重合),過F點的反比例函數y=
如圖所示的平面直角坐標系.F是邊BC上的一個動點(不與B,C重合),過F點的反比例函數y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直線為x軸和y軸,建立如圖所示的平面直角坐標系.F是BC上的一個動點(不與B、C重合),過F點的反比例函數y=
在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直線為x軸和y軸,建立如圖所示的平面直角坐標系.F是BC上的一個動點(不與B、C重合),過F點的反比例函數y=| k |
| x |
| 4 |
| 9 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在矩形AOBC中,OB=4,OA=3,分別以OB、OA所在直線為x軸、y軸建立平面直角坐標系.F是BC邊上的點,過F點的反比例函數y=
如圖,在矩形AOBC中,OB=4,OA=3,分別以OB、OA所在直線為x軸、y軸建立平面直角坐標系.F是BC邊上的點,過F點的反比例函數y=| k | x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com