
【題目】如圖1,已知A![]() ,B
,B![]() 是一次函數y=kx+b與反比例函數
是一次函數y=kx+b與反比例函數![]() 圖象的兩個交點.
圖象的兩個交點.

(1) 根據圖象回答:當x滿足 ,一次函數的值小于反比例函數的值;
(2) 將直線AB沿y軸方向,向下平移n個單位,與雙曲線![]() 有唯一的公共點時,求n的值;
有唯一的公共點時,求n的值;
(3) 如圖2,P點在![]() 的圖象上,矩形OCPD的兩邊OD、OC在坐標軸上,且OC=2OD,M、N分別為OC、OD的中點,PN與DM交于點E,直接寫出四邊形EMON的面積為 .
的圖象上,矩形OCPD的兩邊OD、OC在坐標軸上,且OC=2OD,M、N分別為OC、OD的中點,PN與DM交于點E,直接寫出四邊形EMON的面積為 .
【答案】(1) ![]() <
<![]() 或
或![]() <
<![]() <
<![]() ;(2)
;(2) ![]() 或
或![]() ;(3) 四邊形EMON的面積為
;(3) 四邊形EMON的面積為![]() .
.
【解析】
(1)由![]() 、
、![]() 點的坐標,結合圖象可求得答案;
點的坐標,結合圖象可求得答案;
(2)由待定系數法可求得直線![]() 和反比例函數解析式,可設出向下平移后的直線解析式,聯立該直線與反比例函數解析式,消去
和反比例函數解析式,可設出向下平移后的直線解析式,聯立該直線與反比例函數解析式,消去![]() ,得到關于
,得到關于![]() 的一元二次方程,由判別式等于0可得到關于
的一元二次方程,由判別式等于0可得到關于![]() 的方程,可求得
的方程,可求得![]() 的值;
的值;
(3)由條件可求得![]() 點坐標,則可求得直線
點坐標,則可求得直線![]() 、
、![]() 的解析式,聯立兩直線解析式可求得
的解析式,聯立兩直線解析式可求得![]() 點坐標,過
點坐標,過![]() 作
作![]() 軸于點
軸于點![]() ,利用S四邊形EMON=S△MEG+S梯形ODEG可求得答案.
,利用S四邊形EMON=S△MEG+S梯形ODEG可求得答案.
解:(1)一次函數的值小于反比例函數的值即直線在反比例函數圖象的下方時對應的x的取值范圍,
由圖象可知![]() 的取值范圍為
的取值范圍為![]() 或
或![]() ,
,
故答案為:![]() 或
或![]() ;
;
(2)把![]() 、
、![]() 兩點坐標代入
兩點坐標代入![]() 可得
可得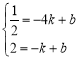 ,
,
解得![]() ,
,
![]() 直線
直線![]() 解析式為
解析式為![]() ,
,
把![]() 點坐標代入反比例函數解析式可得
點坐標代入反比例函數解析式可得![]() ,
,
![]() 反比例函數解析式為
反比例函數解析式為![]() ,
,
設平移后的直線解析式為![]() ,
,
聯立該直線與反比例函數解析式可得
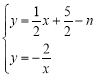 ,
,
消去![]() 整理可得
整理可得![]() ,
,
![]() 直線與雙曲線有唯一的公共點,
直線與雙曲線有唯一的公共點,
![]() △
△![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ;
;
(3)![]() 點
點![]() 在
在![]() 上,
上,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點,
![]() ,
,![]() ,
,
由待定系數法可求得直線![]() 的解析式為
的解析式為![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,
,
聯立兩直線解析式可得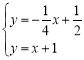 ,
,
解得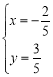 ,
,
![]() ,
,![]() ,
,
過![]() 作
作![]() 軸于點
軸于點![]() ,如圖,
,如圖,
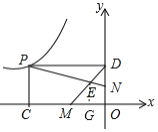
∴S四邊形EMON
=S△MEG+S梯形ODEG
![]()
![]()
![]()
![]() ,
,
故答案為:![]() .
.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案科目:初中數學 來源: 題型:
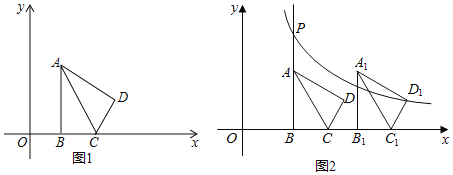
【題目】如圖1,在平面直角坐標系xOy中,已知△ABC,∠ABC=90°,頂點A在第一象限,B,C在x軸的正半軸上(C在B的右側),BC=2,AB=2![]() ,△ADC與△ABC關于AC所在的直線對稱.
,△ADC與△ABC關于AC所在的直線對稱.
(1)當OB=2時,求點D的坐標;
(2)若點A和點D在同一個反比例函數的圖象上,求OB的長;
(3)如圖2,將第(2)題中的四邊形ABCD向右平移,記平移后的四邊形為A1B1C1D1,過點D1的反比例函數y=![]() (k≠0)的圖象與BA的延長線交于點P.問:在平移過程中,是否存在這樣的k,使得以點P,A1,D為頂點的三角形是直角三角形?若存在,請直接寫出所有符合題意的k的值;若不存在,請說明理由.
(k≠0)的圖象與BA的延長線交于點P.問:在平移過程中,是否存在這樣的k,使得以點P,A1,D為頂點的三角形是直角三角形?若存在,請直接寫出所有符合題意的k的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
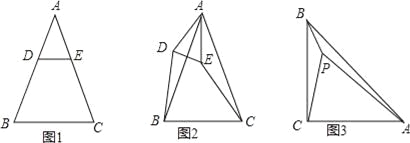
【題目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如圖1,當DE∥BC時,有DB EC.(填“>”,“<”或“=”)
(2)發現探究:若將圖1中的△ADE繞點A順時針旋轉α(0°<α<180°)到圖2位置,則(1)中的結論還成立嗎?若成立,請給予證明;若不成立,請說明理由.
(3)拓展運用:如圖3,P是等腰直角三角形ABC內一點,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某酒店計劃購買一批換氣扇,已知購買2臺![]() 型換氣扇和2臺
型換氣扇和2臺![]() 型換氣扇共需220元;購買3臺
型換氣扇共需220元;購買3臺![]() 型換氣扇和1臺
型換氣扇和1臺![]() 型換氣扇共需200元.
型換氣扇共需200元.
(1)求![]() 兩種型號的換氣扇的單價.
兩種型號的換氣扇的單價.
(2)若該酒店準備同時購進這兩種型號的換氣扇共60臺,并且![]() 型換氣扇的數量不多于
型換氣扇的數量不多于![]() 型換氣扇數量的2倍,請設計出最省錢的購買方案,并說明理由.
型換氣扇數量的2倍,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
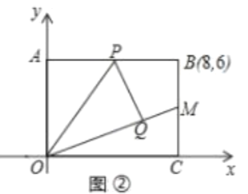
【題目】將矩形紙片放![]() 在平面直角坐標系中,
在平面直角坐標系中,![]() 為坐標原點,點
為坐標原點,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標是
的坐標是![]() ,點
,點![]() 是邊
是邊![]() 上的-一個動點,將
上的-一個動點,將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在點
落在點![]() 處.
處.
![]() 如圖①.當點
如圖①.當點![]() 恰好落在
恰好落在![]() 上時,求點
上時,求點![]() 的坐標;
的坐標;
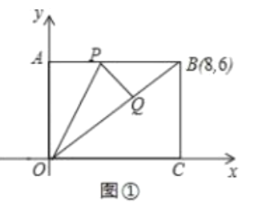
(2)如圖②,當點![]() 是
是![]() 中點時,直線
中點時,直線![]() 交
交![]() 于
于![]() 點,
點,
![]() 求證:
求證:![]() ;
;
![]() 求點
求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】京九鐵路“南昌到贛州”段是連接省會城市與江西南大門城市的重要通道.一列快車從南昌開往贛州,列慢車從贛州開往南昌,兩車同時出發,設慢車行駛的時間為![]() ,兩車之間的距離為
,兩車之間的距離為![]() ,圖中的折線表示
,圖中的折線表示![]() 與
與![]() 之間的函數關系.
之間的函數關系.
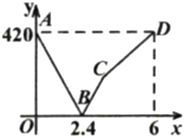
(1)慢車的速度為________![]() ,快車的速度為________
,快車的速度為________![]() ;
;
(2)當快車到達終點贛州后,求![]() 與
與![]() 之間的函數關系.
之間的函數關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把具有一條公共邊的兩個三角形稱為“友鄰三角形”,兩個三角形的公共邊所對的頂點稱為“友鄰頂點”.
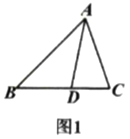
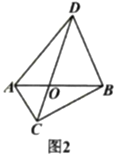
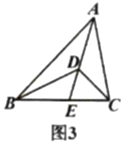
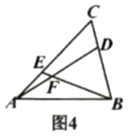
(1)如圖1,寫出圖中所有的“友鄰三角形”;
(2)如圖2,![]() 與
與![]() 相交于點
相交于點![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求證:
,求證:![]() ;
;
(3)從圖3中找出兩對“友鄰三角形”,探索是否存在(2)中類似的結論,并直接寫出結果;
(4)如圖4,![]() ,
,![]() ,若
,若![]() 的面積為21,求
的面積為21,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
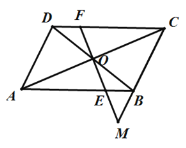
【題目】如圖,ABCD的對角線AC,BD相交于點O,EF經過點O,分別交AB,CD于點E,F,FE的延長線交CB的延長線于點M.
(1)求證:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學利用數學知識測量建筑物DEFG的高度.他從點![]() 出發沿著坡度為
出發沿著坡度為![]() 的斜坡AB步行26米到達點B處,用測角儀測得建筑物頂端
的斜坡AB步行26米到達點B處,用測角儀測得建筑物頂端![]() 的仰角為37°,建筑物底端
的仰角為37°,建筑物底端![]() 的俯角為30°,若AF為水平的地面,側角儀豎直放置,其高度BC=1.6米,則此建筑物的高度DE約為(精確到
的俯角為30°,若AF為水平的地面,側角儀豎直放置,其高度BC=1.6米,則此建筑物的高度DE約為(精確到![]() 米,參考數據:
米,參考數據:![]() ,
,![]() )( )
)( )
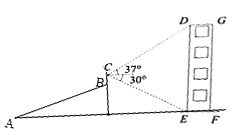
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com