【題目】（本題6分）如圖，已知△ABC，∠C=Rt∠，AC<BC，D為BC上一點，且到A，B兩點的距離相等．
（1）用直尺和圓規，作出點D的位置（不寫作法，保留作圖痕跡）；
（2）連結AD，若∠B=37°，求∠CAD的度數．
科目：初中數學 來源： 題型：
【題目】現計劃把1240噸甲種貨物和880噸乙種貨物用一列火車運往某地，已知這列火車掛有A、B兩種不同規格的貨車車廂共40節，使用A型車廂每節費用為6000元，B型車廂每節費用8000元．如果每節A型車廂最多可裝35噸甲種貨物和15噸乙種貨物，每節B型車廂最多可裝25噸甲種貨物和35噸乙種貨物；
（1）那么共有哪幾種安排車廂的方案？
（2）在上述方案中，哪種方案運費最省、最少運費為多少元？
（3）在（1）問下，若兩種貨物全部售出，且每噸貨物售出獲利200元，除去運費獲
利154000元，問：在這種情況下是按哪種方案安排車廂的.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場計劃購進
、
兩種新型節能臺燈共
盞，這兩種臺燈的進價、售價如表所示：
（
）若商場預計進貨款為
元，則這兩種臺燈各購進多少盞？
（
）若商場規定
型臺燈的進貨數量不超過
型臺燈數量的
倍，應怎樣進貨才能使商場在銷售完這批臺燈時獲利最多？此時利潤為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐
問題背景：
我們知道，三角形的中位線平行于三角形的第三邊，并且等于第三邊的一半，如何證明三角形中位線定理呢?
已知：如圖1，在
中，
分別是
的中點．
求證：
問題中既要證明兩條線段所在的直線平行，又要證明其中一條線段的長等于另一線段長的一半．所以可以用“倍長法”將
延長一倍：延長到
，使得
，連接
這樣只需證明
，且
．由于
是
的中點，容易證明四邊形
、四邊形
是平行四邊形，證明．．．
問題解決：
上述材料中“倍長法”體現的數學思想主要是_____． (填入選項前的字母代號即可)
A．數形結合思想 B．轉化思想 C．分類討論思想 D．方程思想
證明四邊形是平行四邊形的依據是
反思交流：
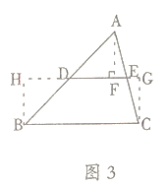
“智慧小組”在證明中位線定理時，在圖1的基礎上追加了如上輔助線作法：如圖3，分別過點
作的垂線，垂足分別為
，．．
請你根據“智慧小組”添加的輔助線，證明三角形的中位線定理．
方法遷移：
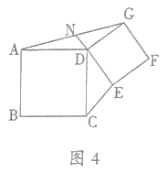
如圖4、四邊形
和
都是正方形，
是
的中點．求證： 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】《九章算術》是中國古代數學專著，在數學上有其獨到的成就，不僅最早提到了分數問題，也首先記錄了“盈不足”等問題．如有一道闡述“盈不足”的問題，原文如下：今有共買雞，人出九，盈十一；人出六，不足十六．問人數、雞價各幾何？譯文為：現有若干人合伙出錢買雞，如果每人出9文錢，就會多11文錢；如果每人出6文錢，又會缺16文錢．問買雞的人數、雞的價格各是多少？請解答上述問題．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形網格圖中建立一直角坐標系，一條圓弧經過網格點A、B、C，請在網格中進行下列操作：
（1）請在圖中確定該圓弧所在圓心D點的位置，D點坐標為 ；
（2）連接AD、CD，求⊙D的半徑及扇形DAC的圓心角度數；
（3）若扇形DAC是某一個圓錐的側面展開圖，求該圓錐的底面半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，CD⊥AB于點D，DA=DC=4，DB=2，AF⊥BC于點F，交DC于點E．
（1）求線段AE的長；
（2）若點G是AC的中點，點M是線段CD上一動點，連結GM，過點G作GN⊥GM交直線AB于點N，記△CGM的面積為S1，△AGN的面積為S2．在點M的運動過程中，試探究：S1與S2的數量關系
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】正方形ABCD內接于⊙O，如圖所示，在劣弧
上取一點E，連接DE、BE，過點D作DF∥BE交⊙O于點F，連接BF、AF，且AF與DE相交于點G，求證：
（1）四邊形EBFD是矩形；
（2）DG=BE．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
