Question

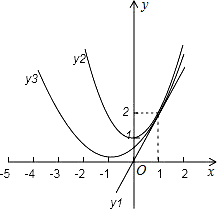
已知一次函數y₁=2x和二次函數y₂=x²+1．
（1）求證：函數y₁、y₂的圖象都經過同一個定點；
（2）求證：在實數范圍內，對于任意同一個x的值，這兩個函數所對應的函數值y₁≤y₂總成立；
（3）是否存在拋物線y₃=ax²+bx+c，其圖象經過點（-5，2），且在實數范圍內，對于同一個x的值，這三個函數所對應的函數值y₁≤y₃≤y₂總成立？若存在，求出y₃的解析式；若不存在，說明理由．

Answer 1

解：（1）令y₁=y₂，
得：2x=x²+1，
整理得：x²-2x+1=0
∵△=b²-4ac=（-2）²-4=0
∴直線y₁=2x與拋物線y₂=x²+1只有一個交點，
即：函數y₁、y₂的圖象都經過同一個定點；

（2）在實數范圍內，對于x的同一個值y₂=x²+1=（x-1）²+2x，y₁=2x，
∵（x-1）²≥0，
∴y₁≤y₂；

（3）由y₁=2x，y₂=x²+1得：
y₂-y₁=x²+1-2x=（x-1）²
即當x=1時，有y₁=y₂=2．
所以（1，2）點為y₁和y₂的交點．
因為要滿足y₁≤y₃≤y₂恒成立，所以y₃圖象必過（1，2）點．
又因為y₃-y₁=ax²+bx+c-2x恒大于等于0，即ax²+（b-2）x+c恒大于等于0，所以二次函數ax²+（b-2）x+c必定開口向上，
即有a＞0且（b-2）²-4ac≤0，
同樣有y₂-y₃=（1-a）x²-bx+（1-c）恒大于0，
有 1-a＞0 且 b²-4（1-a）（1-c）≤0，
又因為函數過（-5，2）和（1，2）兩點，所以有
25a-5b+c=2 ①
a+b+c=2 ②
①-②得 b=4a，
將b=4a代入②得：c=2-5a，
代入（b-2）²-4ac≤0得，
（4a-2）²-4a（2-5a）=16a²-16a+4-8a+20a²
=36×a²-24a+4=4（3a-1）²≤0
等式成立時 a=，
將b=4a，c=2-5a 代入b²-4（1-a）（1-c）≤0，
（4a）²-4（1-a）（1-（2-5a））=36×a²-24a+4=4（3a-1）²≤0
滿足條件a=
所以y₃的解析式為y₃=（x²+4a+1）=x2+x+．
分析：（1）令y₁=y₂，得到2x=x²+1，得到其根的判別式等于0即可說明兩圖象只有一個交點，即經過同一個定點．
（2）把y₂化成完全平方的形式與y₁進行比較即可得出結論；
（3）由圖可知，在實數范圍內，對于x的同一個值，三個函數所對應的函數值y₁≤y₃≤y₂均成立，利用c=2-5a，代入（b-2）²-4ac≤0得出a的值，于是可推理出拋物線的解析式．
點評：此題主要考查了二次函數與一元二次方程的關系、根的判別式、完全平方公式、非負數的性質以及用待定系數法確定函數解析式的方法，難度較大．