
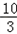 )秒.解答如下問題:
)秒.解答如下問題: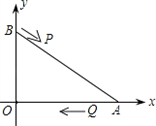
解:(1)∵A、B兩點的坐標分別是(8,0)、(0,6),
則OB=6,OA=8,
∴AB=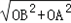 =
= =10.
=10.
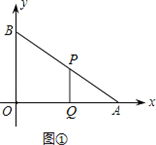
如圖①,當PQ∥BO時,AQ=2t,BP=3t,則AP=10﹣3t.
∵PQ∥BO,∴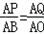 ,即
,即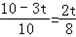 ,解得t=
,解得t=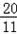 ,
,
∴當t=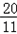 秒時,PQ∥BO.
秒時,PQ∥BO.
(2)由(1)知:OA=8,OB=6,AB=10.
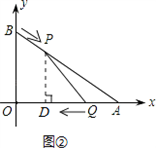
①如圖②所示,過點P作PD⊥x軸于點D,則PD∥BO,
∴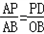 ,即
,即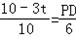 ,
,
解得PD=6﹣ t.S=
t.S= AQPD=
AQPD= ×2t×(6﹣
×2t×(6﹣ t)=6t﹣
t)=6t﹣ t2=﹣
t2=﹣ (t﹣
(t﹣ )2+5,
)2+5,
∴S與t之間的函數關系式為:S=﹣ (t﹣
(t﹣ )2+5(0<t<
)2+5(0<t<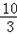 ),
),
當t= 秒時,S取得最大值,最大值為5(平方單位).
秒時,S取得最大值,最大值為5(平方單位).
②如圖②所示,當S取最大值時,t= ,∴PD=6﹣
,∴PD=6﹣ t=3,
t=3,
∴PD= BO,
BO,
又PD∥BO,
∴此時PD為△OAB的中位線,則OD= OA=4,
OA=4,
∴P(4,3).又AQ=2t=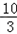 ,∴OQ=OA﹣AQ=
,∴OQ=OA﹣AQ=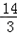 ,∴Q(
,∴Q(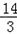 ,0).
,0).
依題意,“向量PQ”的坐標為(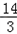 ﹣4,0﹣3),即(
﹣4,0﹣3),即( ,﹣3).
,﹣3).
∴當S取最大值時,“向量PQ”的坐標為( ,﹣3).
,﹣3).


科目:初中數學 來源: 題型:
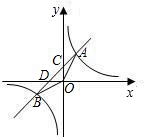 如圖,一次函數y=kx+b的圖象經過第一、二、三象限,且與反比例函數圖象相交于A,B兩點,與y軸交于點C,與x軸交于點D,OB=
如圖,一次函數y=kx+b的圖象經過第一、二、三象限,且與反比例函數圖象相交于A,B兩點,與y軸交于點C,與x軸交于點D,OB=| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 20、當你去看電影的時候,你想坐得離屏幕近一些,可是又不想為了看屏幕邊緣的鏡頭不停地轉動眼睛.如圖所示,點A、B分別為屏幕邊緣兩點,若你在P點,則視角為∠APB.如果你覺得電影院內P點是觀看的最佳位置,可是已經有人坐在那了,那么你會找到一個位置Q,使得在Q、P兩點有相同的視角嗎?請在圖中畫出來(保留畫圖痕跡,不寫畫法).
20、當你去看電影的時候,你想坐得離屏幕近一些,可是又不想為了看屏幕邊緣的鏡頭不停地轉動眼睛.如圖所示,點A、B分別為屏幕邊緣兩點,若你在P點,則視角為∠APB.如果你覺得電影院內P點是觀看的最佳位置,可是已經有人坐在那了,那么你會找到一個位置Q,使得在Q、P兩點有相同的視角嗎?請在圖中畫出來(保留畫圖痕跡,不寫畫法).查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•河北一模)如圖,已知直線y=x+4與兩坐???軸分別交于A、B兩點,⊙C的圓心坐標為 (2,O),半徑為2,若D是⊙C上的一個動點,線段DA與y軸交于點E,則△ABE面積的最小值和最大值分別是
(2013•河北一模)如圖,已知直線y=x+4與兩坐???軸分別交于A、B兩點,⊙C的圓心坐標為 (2,O),半徑為2,若D是⊙C上的一個動點,線段DA與y軸交于點E,則△ABE面積的最小值和最大值分別是| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com