
【題目】目前“微信”、“支付寶”、“共享單車”和“網購”給我們的生活帶來了很多便利,初二數學小組在校內對“你最認可的四大新生事物”進行調查,隨機調查了![]() 人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.
人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.
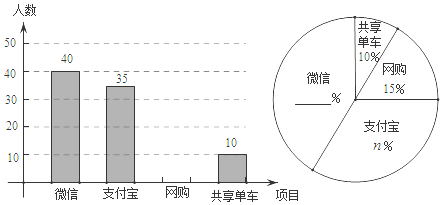
(1)根據圖中的信息求出![]() _______,
_______,![]() _______;
_______;
(2)請你幫助他們將這兩個統計圖補全,并計算扇形統計圖中“支付寶”部分所對應的圓心角的度數為_____;
(3)根據抽樣調查的結果,請估算全校2000名學生中,大約有多少人最認可“微信”這一新生事物?
【答案】(1)![]() 100,
100,![]() 35;(2)126°;(3)大約有800人最認可“微信”這一新生事物.
35;(2)126°;(3)大約有800人最認可“微信”這一新生事物.
【解析】
(1)利用選擇共享單車的人數和所占百分比可求出m的值,進而可求出選擇支付寶的人數所占百分比,即可得n的值;
(2)用總人數m乘以網購所占百分比即可求出選擇網購的人數,可補全條形統計圖,根據共享單車、網購、支付寶所占百分比即可求出微信所占百分比,補全扇形統計圖即可;根據支付寶所占百分比乘以360°即可求出對應的圓心角的度數;
(3)用2000乘以微信所占百分比即可得答案.
(1)m=10÷10%=100,
35÷100=35%,即n=35,
故答案為:100,35
(2)選擇網購的人數為:100×15%=15(人),
微信所占百分比為:1-10%-15%-35%=40%,
∴補全兩個統計圖如下:
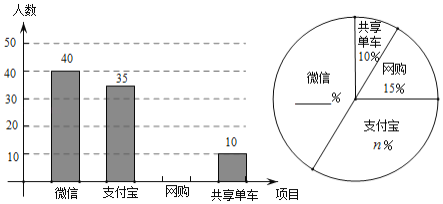
“支付寶”部分所對應的圓心角的度數為360°×35%=126°;
故答案為:126°
(3)2000×40%=800(人).
答:大約有800人最認可“微信”這一新生事物.


科目:初中數學 來源: 題型:
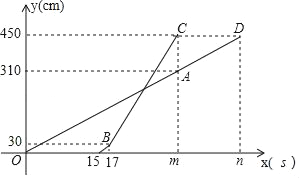
【題目】甲、乙兩臺智能機器人從同一地點出發,沿著筆直的路線行走了450cm.甲比乙先出發,并且勻速走完全程,乙出發一段時間后速度提高為原來的2倍.設甲行走的時間為x(s),甲、乙行走的路程分別為y1(cm)、y2(cm),y1、y2與x之間的函數圖象如圖所示,根據圖象所提供的信息解答下列問題:
(1)乙比甲晚出發 s,乙提速前的速度是每秒 cm,m= ,n= ;
(2)當x為何值時,乙追上了甲?
(3)在乙提速后到甲、乙都停止的這段時間內,當甲、乙之間的距離不超過20cm時,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
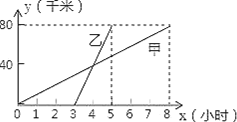
【題目】甲、乙兩人分別騎自行車和摩托車沿相同路線由A地到相距80千米的B地,行駛過程中的函數圖象如圖所示,請根據圖象回答下列問題:
(1)甲先出發______小時后,乙才出發;大約在甲出發______小時后,兩人相遇,這時他們離A地_______千米.
(2)兩人的行駛速度分別是多少?
(3)分別寫出表示甲、乙的路程y(千米)與時間x(小時)之間的函數表達式(不要求寫出自變量的取值范圍).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是直線y=3上的動點,連接PO并將PO繞P點旋轉90°到PO′,當點O′剛好落在雙曲線![]() (x>0)上時,點P的橫坐標所有可能值為_____.
(x>0)上時,點P的橫坐標所有可能值為_____.
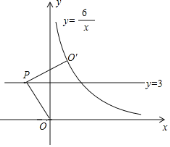
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班級準備購買一些獎品獎勵春季運動會表現突出的同學,獎品分為甲、乙兩種,已知,購買一個甲獎品比一個乙獎品多用20元,若用400元購買甲獎品的個數是用160元購買乙獎品個數的一半.
(1)求購買一個甲獎品和一個乙獎品各需多少元?
(2)經商談,商店決定給予該班級每購買甲獎品3個就贈送一個乙獎品的優惠,如果該班級需要乙獎品的個數是甲獎品的2倍還多8個,且該班級購買兩種獎項的總費用不超過640元,那么該班級最多可購買多少個甲獎品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為6的正方形ABCD中,E是邊CD的中點,將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG.
(1)求證:△ABG≌△AFG;(2)求BG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個長方體紙盒的平面展開圖,已知紙盒中相對兩個面上的數互為相反數.
(1)填空:a= ,b= ,c= ;
(2)先化簡,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,矩形
中,矩形![]() 的頂點
的頂點![]() 在
在![]() 軸的正半軸上,頂點
軸的正半軸上,頂點![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,![]() 是
是![]() 邊上的一點,
邊上的一點,![]() ,
,![]() .反比例函數
.反比例函數![]() 在第一象限內的圖像經過點
在第一象限內的圖像經過點![]() ,交
,交![]() 于點
于點![]() ,
,![]() .
.
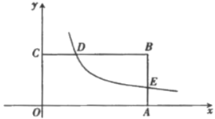
(1)求這個反比例函數的表達式,
(2)動點![]() 在矩形
在矩形![]() 內,且滿足
內,且滿足![]() .
.
①若點![]() 在這個反比例函數的圖像上,求點
在這個反比例函數的圖像上,求點![]() 的坐標,
的坐標,
②若點![]() 是平面內一點,使得以
是平面內一點,使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形,求點
為頂點的四邊形是菱形,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠AFC,以下結論:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=![]() ∠BAC,其中正確的結論有_____________。
∠BAC,其中正確的結論有_____________。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com