
【題目】已知,直線l1:y=﹣x+n過點A(﹣1,3),雙曲線C:y= ![]() (x>0),過點B(1,2),動直線l2:y=kx﹣2k+2(常數k<0)恒過定點F.
(x>0),過點B(1,2),動直線l2:y=kx﹣2k+2(常數k<0)恒過定點F.
(1)求直線l1 , 雙曲線C的解析式,定點F的坐標;
(2)在雙曲線C上取一點P(x,y),過P作x軸的平行線交直線l1于M,連接PF.求證:PF=PM.
(3)若動直線l2與雙曲線C交于P1 , P2兩點,連接OF交直線l1于點E,連接P1E,P2E,求證:EF平分∠P1EP2 .
【答案】
(1)解:∵直線l1:y=﹣x+n過點A(﹣1,3),
∴﹣(﹣1)+n=3,
解得:n=2,
∴直線l1的解析式為:y=﹣x+2
∵雙曲線C:y= ![]() (x>0)過點B(1,2),
(x>0)過點B(1,2),
∴m=xy=1×2=2,
即雙曲線C的解析式為:y= ![]() ,
,
∵動直線l2:y=kx﹣2k+2=k(x﹣2)+2,
∴不論k為任何負數時,當x=2時,則y=2,
即動直線l2:y=kx﹣2k+2恒過定點F(2,2)
(2)解:證明:如圖1,在雙曲線C上任取一點P(x,y),過P作x軸的平行線交直線l1于M(x0,y),連接PF.
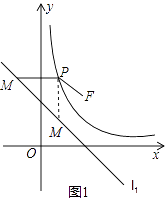
則PF=x﹣x0,
又∵M(x0,y)在直線l1上,
∴﹣x0+2=y,
∴x0=2﹣y=2﹣ ![]() ,
,
∴PM=x+ ![]() ﹣2,
﹣2,
又∵PF= ![]() =
= ![]() =
= ![]() =
= ![]() =x+
=x+ ![]() ﹣2;
﹣2;
(注:x+ ![]() ﹣2=(
﹣2=( ![]() )2+(
)2+( ![]() )2﹣2
)2﹣2 ![]()
![]() +2
+2 ![]() ﹣2=(
﹣2=( ![]() ﹣
﹣ ![]() )2+2
)2+2 ![]() ﹣2=(
﹣2=( ![]() ﹣
﹣ ![]() )2+2(
)2+2( ![]() ﹣1)≥2(
﹣1)≥2( ![]() ﹣1)>0)
﹣1)>0)
∴PM=PF
(3)解:證明:如圖2,過P1分別作P1M1∥x軸交l1span>于M1,作P1N1⊥l1,垂足為N1,過P2分別作P2M2∥x軸交l1于M2,作P2N2⊥l1,垂足為N2,
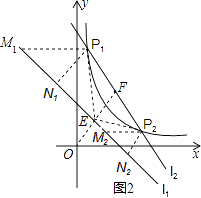
∵直線l1的解析式為y=﹣x+2,
∴△P1M1N1和△P2M2N2都是等腰直角三角形.
∴P1N1= ![]() P1M1=
P1M1= ![]() P1F,P2N2=
P1F,P2N2= ![]() P2M2=
P2M2= ![]() P2F,
P2F,
∵直線EF的解析為:y=x,
∴EF⊥l1,
∴P1N1∥EF∥P2N2,
∴ ![]() =
= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴△P1N1E∽△P2N2E,
∴∠P1EN1=∠P2EN2,
∵∠P1EF=90°﹣∠P1EN1,∠P2EF=90°﹣∠P2EN2,
∴∠P1EF=∠P2EF,
∴EF平分∠P1EP2
【解析】本題是反比例函數綜合題,考查了待定系數法求函數解析式、勾股定理、等腰直角三角形的性質、相似三角形的判定與性質,準確作出輔助線是解題的關鍵.
【考點精析】本題主要考查了反比例函數的性質的相關知識點,需要掌握性質:當k>0時雙曲線的兩支分別位于第一、第三象限,在每個象限內y值隨x值的增大而減小; 當k<0時雙曲線的兩支分別位于第二、第四象限,在每個象限內y值隨x值的增大而增大才能正確解答此題.


科目:初中數學 來源: 題型:
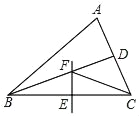
【題目】如圖,△ABC中,BD平分∠ABC,BC的中垂線交BC于點E,交BD于點F,連接CF.若∠A=60°,∠ACF=42°,則∠ABC=_____°.
查看答案和解析>>
科目:初中數學 來源: 題型:
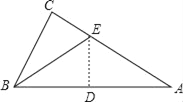
【題目】有一直角三角形紙片,∠C=90°,BC=6,AC=8,現將△ABC按如圖那樣折疊,使點A與點B重合,折痕為DE,則CE的長為( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是AB的中點,點D是BC的中點,現給出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正確的等式編號是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正確的等式編號是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把四張大小相同的長方形卡片(如圖①)按圖②、圖③兩種放法放在一個底面為長方形(長比寬多6)的盒底上,底面未被卡片覆蓋的部分用陰影表示,若記圖②中陰影部分的周長為C2,圖③中陰影部分的周長為C3,則C2-C3=______.
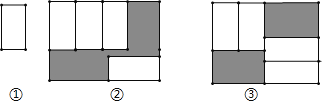
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,對角線AC、BD相交于點O,BD=2AD,E、F、G分別是OC、OD、AB的中點,下列結論:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四邊形BEFG是菱形.其中正確的個數是( )
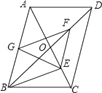
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com