Question

如下圖，A、B兩點都與平面鏡相距4米，且A、B兩點相距6米，一束光線由A射向平面鏡反射之后恰巧經過B點.求B點到入射點的距離.

 

Answer 1

【答案】

5米

【解析】

試題分析：作出B點關于CD的對稱點B′，連結AB′，交CD于點O，則O點就是光的入射點，先根據“SSS”證得△B′DO≌△ACO，即可求得OC、OD的長，

連結OB，在Rt△ODB中，根據勾股定理即可求得結果.

作出B點關于CD的對稱點B′，連結AB′，交CD于點O，則O點就是光的入射點.

因為B′D=DB.

所以B′D=AC.

∠B′DO=∠OCA=90°，

∠B′=∠CAO

所以△B′DO≌△ACO(SSS)

則OC=OD=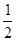AB=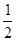×6=3米.

連結OB，在Rt△ODB中，OD²+BD²=OB²

所以OB²=3²+4²=5²，即OB=5(米).

所以點B到入射點的距離為5米.

考點：本題考查的是勾股定理的應用

點評：這是以光的反射為背景的一道綜合題，涉及到許多幾何知識，由此可見，數學是學習物理的基礎.