
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江省金華四中九年級畢業生學業考試模擬數學卷(帶解析) 題型:解答題
如圖1,在等腰梯形ABCO中,AB∥CO,E是AO的中點,過點E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.現把梯形ABCO放置在平面直角坐標系中,使點O與原點重合,OC在x軸正半軸上,點A,B在第一象限內.
(1)求點E的坐標及線段AB的長;
(2)點P為線段EF上的一個動點,過點P作PM⊥EF交OC于點M,過M作MN∥AO交折線ABC于點N,連結PN,設PE=x.△PMN的面積為S.
①求S關于x的函數關系式;
②△PMN的面積是否存在最大值,若不存在,請說明理由.若存在,求出面積的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.現在開始操作:固定等腰梯形ABCO,將直角梯形EDGH以每秒1個單位的速度沿OC方向向右移動,直到點D與點C重合時停止(如圖2).設運動時間為t秒,運動后的直角梯形為E′D′G′H′(如圖3);試探究:在運動過程中,等腰梯ABCO與直角梯形E′D′G′H′重合部分的面積y與時間t的函數關系式.
查看答案和解析>>
科目:初中數學 來源:2012屆浙江省江山市中考一模數學試卷(帶解析) 題型:解答題
如圖1,在等腰梯形ABCD中,AB∥CO,E是AO的中點,過點E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.現把梯形ABCO放置在平面直角坐標系中,使點O與原點重合,OC在x軸正半軸上,點A、B在第一象限內。
(1) 求點E的坐標;
(2) 點P為線段EF上的一個動點,過點P作PM⊥EF交OC于點M,過M作MN∥AO交折線ABC于點N,
連結PN。設PE=x.△PMN的面積為S。
① 求S關于x的函數關系式;
② △PMN的面積是否存在最大值,若不存在,請說明理由。若存在,求出面積的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC)。現在開始操作:固定等腰梯形ABCO,將直角梯形EDGH以每秒1個單位的速度沿OC方向向右移動,直到點D與點C重合時停止(如圖2)。設運動時間為t秒,運動后的直角梯形為E′D′G′H′;探究:在運動過程中,等腰梯形ABCO與直角梯形E′D′G′H′重合部分的面積y與時間t的函數關系式。


查看答案和解析>>
科目:初中數學 來源:2012屆浙江省九年級畢業生學業考試模擬數學卷(解析版) 題型:解答題
如圖1,在等腰梯形ABCO中,AB∥CO,E是AO的中點,過點E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.現把梯形ABCO放置在平面直角坐標系中,使點O與原點重合,OC在x軸正半軸上,點A,B在第一象限內.
(1)求點E的坐標及線段AB的長;
(2)點P為線段EF上的一個動點,過點P作PM⊥EF交OC于點M,過M作MN∥AO交折線ABC于點N,連結PN,設PE=x.△PMN的面積為S.
①求S關于x的函數關系式;
②△PMN的面積是否存在最大值,若不存在,請說明理由.若存在,求出面積的最大值;
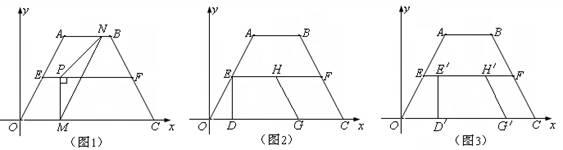
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.現在開始操作:固定等腰梯形ABCO,將直角梯形EDGH以每秒1個單位的速度沿OC方向向右移動,直到點D與點C重合時停止(如圖2).設運動時間為t秒,運動后的直角梯形為E′D′G′H′(如圖3);試探究:在運動過程中,等腰梯ABCO與直角梯形E′D′G′H′重合部分的面積y與時間t的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com