
【題目】已知OA是⊙O的半徑,OA=1,點P是OA上一動點,過P作弦BC⊥OA,連接AB、AC.
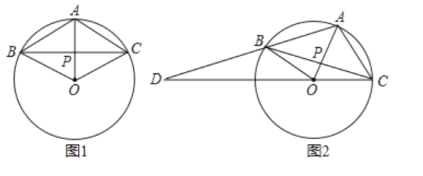
(1)如圖1,若P為OA中點,則AC=______,∠ACB=_______°;
(2)如圖2,若移動點P,使AB、CO的延長線交于點D.記△AOC的面積為S1,△BOD的面積為S2.△AOD的面積為S3,且滿足![]() ,求
,求![]() 的值.
的值.
【答案】(1)1,30;(2)![]() .
.
【解析】
(1)證得△AOC為等邊三角形,得出AC=1,∠ACO=60°,可求出答案;
(2)若DC與圓O相交于點E,連接BE,證明△ABO≌△ACO(SSS),得出S△ABO=S△ACO=S1,由題意得出(![]() )2+
)2+![]() 1=0,解得:
1=0,解得:![]() =
=![]() ,求出
,求出![]() ,證明△AOD∽△BED,得出
,證明△AOD∽△BED,得出![]() =
=![]() ,得出OP=
,得出OP=![]() BE,則可求出答案.
BE,則可求出答案.
解:(1)∵BC⊥OA,OB=OC,
∴BP=CP,
∵P是OA的中點,
∴OP=AP,
∴OA垂直平分BC,且BC垂直平分OA,
∴四邊形ABOC是菱形,
∴AC=OC=OA=1,BC平分∠ACO,
∴△AOC是等邊三角形,
∴∠ACO=60°,
∴∠ACB=![]() ∠ACO=30°,
∠ACO=30°,
故答案為:1,30;
(2)連接![]() ,
,

∵![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,AO=AO,
,AO=AO,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴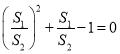 ,
,
解得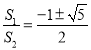 ,
, ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 為直徑,
為直徑,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】我們把有一組鄰邊相等,一組對邊平行但不相等的四邊形稱作“準菱形”.
(1)證明“準菱形”性質:“準菱形”的一條對角線平分一個內角.
(要求:根據圖1寫出已知,求證,證明)
已知:
求證:
證明:
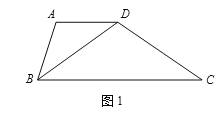
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若點D,E分別在邊BC,AC上,且四邊形ABDE為“準菱形”.請在下列給出的△ABC中,作出滿足條件的所有“準菱形”ABDE,并寫出相應DE的長.(所給△ABC不一定都用,不夠可添)
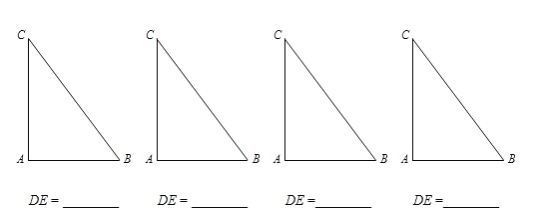
查看答案和解析>>
科目:初中數學 來源: 題型:
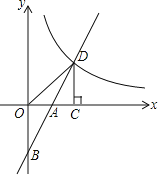
【題目】如圖,在平面直角坐標系中,直線![]() 與坐標軸交于
與坐標軸交于![]() 兩點,與反比例函數
兩點,與反比例函數![]() 的圖象交于
的圖象交于![]() 點,過點
點,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,連接
,連接![]() .已知
.已知![]() .
.
(1)如果![]() ,求
,求![]() 的值;
的值;
(2)試探究![]() 與
與![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】參照學習函數的過程方法,探究函數![]() 的圖像與性質,因為
的圖像與性質,因為![]() ,即
,即![]() ,所以我們對比函數
,所以我們對比函數![]() 來探究列表:
來探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描點:在平面直角坐標系中以自變量![]() 的取值為橫坐標,以
的取值為橫坐標,以![]() 相應的函數值為縱坐標,描出相應的點如圖所示:
相應的函數值為縱坐標,描出相應的點如圖所示:
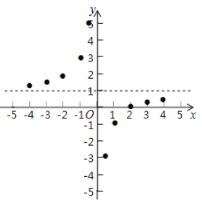
(1)請把![]() 軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
(2)觀察圖象并分析表格,回答下列問題:
①當![]() 時,
時,![]() 隨
隨![]() 的增大而______;(“增大”或“減小”)
的增大而______;(“增大”或“減小”)
②![]() 的圖象是由
的圖象是由![]() 的圖象向______平移______個單位而得到的;
的圖象向______平移______個單位而得到的;
③圖象關于點______中心對稱.(填點的坐標)
(3)函數![]() 與直線
與直線![]() 交于點
交于點![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察以下等式:
第1個等式:23-22=13+2×1+1;
第2個等式:33-32=23+3×2+22;
第3個等式:43-42=33+4×3+32;
……
按照以上規律,解決下列問題:
(1)寫出第4個等式:__________________;
(2)寫出你猜想的第n個等式(用含n的等式表示),并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
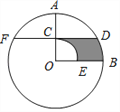
【題目】如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且CD=![]() ,以O為圓心,OC為半徑作
,以O為圓心,OC為半徑作![]() ,交OB于E點.則圖中陰影部分的面積為______________.
,交OB于E點.則圖中陰影部分的面積為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“南昌之星”摩天輪,位于江西省南昌市紅谷灘新區紅角洲贛江邊上的贛江市民公園,摩天輪高160m(最高點到地面的距離).如圖,點O是摩天輪的圓心,AB是其垂直于地面的直徑,小賢在地面點C處利用測角儀測得摩天輪的最高點A的仰角為45°,測得圓心O的仰角為30°,則摩天輪的半徑為_____m.(結果保留根號)
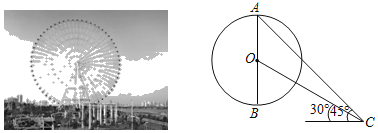
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區山峰的高度每增加1百米,氣溫大約降低0.6℃.氣溫T(℃)和高度h(百米)的函數關系如圖所示.請根據圖象解決下列問題:
(1)求高度為5百米時的氣溫.
(2)求T關于h的函數表達式.
(3)測得山頂的氣溫為6℃,求該山峰的高度.
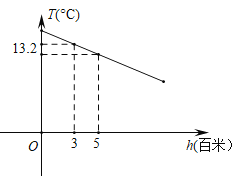
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過點A(﹣1,0),B(4,0),C(0,2)三點,點D與點C關于![]() 軸對稱,點P是
軸對稱,點P是![]() 軸上的一個動點,設點P的坐標為(
軸上的一個動點,設點P的坐標為(![]() ,0),過點P做
,0),過點P做![]() 軸的垂線l交拋物線于點Q,交直線BD于點M.
軸的垂線l交拋物線于點Q,交直線BD于點M.
(1)求該拋物線所表示的二次函數的表達式;
(2)點P在線段AB運動過程中,是否存在點Q,使得△BOD∽△QBM?若存在,求出點Q的坐標;若不存在,請說明理由.
(3)已知點F(0,![]() ),當點P在
),當點P在![]() 軸上運動時,試求
軸上運動時,試求![]() 為何值時,以D,M,Q,F為頂點的四邊形是平行四邊形?
為何值時,以D,M,Q,F為頂點的四邊形是平行四邊形?
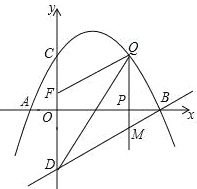
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com