
如圖1,點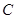 將線段
將線段 分成兩部分,如果
分成兩部分,如果 ,那么稱點
,那么稱點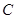 為線段
為線段 的黃金分割點.
的黃金分割點.
某研究小組在進行課題學習時,由黃金分割點聯(lián)想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線 將一個面積為
將一個面積為 的圖形分成兩部分,這兩部分的面積分別為
的圖形分成兩部分,這兩部分的面積分別為 ,
, ,如果
,如果 ,那么稱直線
,那么稱直線 為該圖形的黃金分割線.
為該圖形的黃金分割線.

(1)研究小組猜想:在 中,若點
中,若點 為
為 邊上的黃金分割點(如圖2),則直線
邊上的黃金分割點(如圖2),則直線 是
是 的黃金分割線.你認為對嗎?為什么?
的黃金分割線.你認為對嗎?為什么?
(2)請你說明:三角形的中線是否也是該三角形的黃金分割線?
(3)研究小組在進一步探究中發(fā)現(xiàn):過點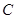 任作一條直線交
任作一條直線交 于點
于點 ,再過點
,再過點 作直線
作直線 ,交
,交 于點
于點 ,連接
,連接 (如圖3),則直線
(如圖3),則直線 也是
也是 的黃金分割線.
的黃金分割線.
請你說明理由.
(4)如圖4,點 是
是 的邊
的邊 的黃金分割點,過點
的黃金分割點,過點 作
作 ,交
,交 于點
于點 ,顯然直線
,顯然直線 是
是 的黃金分割線.請你畫一條
的黃金分割線.請你畫一條 的黃金分割線,使它不經(jīng)過
的黃金分割線,使它不經(jīng)過 各邊黃金分割點.
各邊黃金分割點.
(1)對,理由見解析(2)不可能(3)理由見解析(4)見解析
【解析】(1)直線 是
是 的黃金分割線.理由如下:
的黃金分割線.理由如下:
設 的邊
的邊 上的高為
上的高為 .
.
 ,
, ,
, ,
,
所以, ,
, .··············· 2分
.··············· 2分
又因為點 為邊
為邊 的黃金分割點,所以有
的黃金分割點,所以有 .因此
.因此 .
.
所以,直線 是
是 的黃金分割線.·············· 4分
的黃金分割線.·············· 4分
(2)因為三角形的中線將三角形分成面積相等的兩部分,此時 ,即
,即
 ,所以三角形的中線不可能是該三角形的黃金分割線.········ 6分
,所以三角形的中線不可能是該三角形的黃金分割線.········ 6分
(3)因為 ,所以
,所以 和
和 的公共邊
的公共邊 上的高也相等,
上的高也相等,
所以有 .························· 7分
.························· 7分
設直線 與
與 交于點
交于點 .所以
.所以 .
.
所以
 ,
, .
.
又因為 ,所以
,所以 .··········· 9分
.··········· 9分
因此,直線 也是
也是 的黃金分割線.··············· 10分
的黃金分割線.··············· 10分
(4)畫法不惟一,現(xiàn)提供兩種畫法;·················· 12分

畫法一:如答圖1,取 的中點
的中點 ,再過點
,再過點 作一條直線分別交
作一條直線分別交 ,
, 于
于 ,
, 點,則直線
點,則直線 就是
就是 的黃金分割線.
的黃金分割線.
畫法二:如答圖2,在 上取一點
上取一點 ,連接
,連接 ,再過點
,再過點 作
作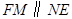 交
交 于點
于點 ,連接
,連接 ,則直線
,則直線 就是
就是 的黃金分割線.
的黃金分割線.
(1)由于 是同高,而點
是同高,而點 為邊
為邊 的黃金分割點,則
的黃金分割點,則 ,所以
,所以 ,故直線
,故直線 是
是 的黃金分割線
的黃金分割線
(2)只需判斷它們面積比是否相等,若相等則中線是三角形的黃金分割線,否則不是
(3)根據(jù)平行線間的距離相等,則 ,通過圖形面積的轉(zhuǎn)化,直線
,通過圖形面積的轉(zhuǎn)化,直線 分三角形的圖形面積有
分三角形的圖形面積有 ,故直線
,故直線 也是
也是 的黃金分割線
的黃金分割線
(4)畫法不惟一,只需分成圖形面積比相等即可


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源:2007年初中畢業(yè)升學考試(江蘇連云港卷)數(shù)學(帶解析) 題型:解答題
如圖1,點 將線段
將線段 分成兩部分,如果
分成兩部分,如果 ,那么稱點
,那么稱點 為線段
為線段 的黃金分割點.
的黃金分割點.
某研究小組在進行課題學習時,由黃金分割點聯(lián)想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線 將一個面積為
將一個面積為 的圖形分成兩部分,這兩部分的面積分別為
的圖形分成兩部分,這兩部分的面積分別為 ,
, ,如果
,如果 ,那么稱直線
,那么稱直線 為該圖形的黃金分割線.
為該圖形的黃金分割線.
(1)研究小組猜想:在 中,若點
中,若點 為
為 邊上的黃金分割點(如圖2),則直線
邊上的黃金分割點(如圖2),則直線 是
是 的黃金分割線.你認為對嗎?為什么?
的黃金分割線.你認為對嗎?為什么?
(2)請你說明:三角形的中線是否也是該三角形的黃金分割線?
(3)研究小組在進一步探究中發(fā)現(xiàn):過點 任作一條直線交
任作一條直線交 于點
于點 ,再過點
,再過點 作直線
作直線 ,交
,交 于點
于點 ,連接
,連接 (如圖3),則直線
(如圖3),則直線 也是
也是 的黃金分割線.
的黃金分割線.
請你說明理由.
(4)如圖4,點 是
是 的邊
的邊 的黃金分割點,過點
的黃金分割點,過點 作
作 ,交
,交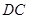 于點
于點 ,顯然直線
,顯然直線 是
是 的黃金分割線.請你畫一條
的黃金分割線.請你畫一條 的黃金分割線,使它不經(jīng)過
的黃金分割線,使它不經(jīng)過 各邊黃金分割點.
各邊黃金分割點.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
如圖1,點![]() 將線段
將線段![]() 分成兩部分,如果
分成兩部分,如果![]() ,那么稱點
,那么稱點![]() 為線段
為線段![]() 的黃金分割點.某研究小組在進行課題學習時,由黃金分割點聯(lián)想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線
的黃金分割點.某研究小組在進行課題學習時,由黃金分割點聯(lián)想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線![]() 將一個面積為
將一個面積為![]() 的圖形分成兩部分,這兩部分的面積分別為
的圖形分成兩部分,這兩部分的面積分別為![]() ,
,![]() ,如果
,如果![]() ,那么稱直線
,那么稱直線![]() 為該圖形的黃金分割線.
為該圖形的黃金分割線.
(1)研究小組猜想:在![]() 中,若點
中,若點![]() 為
為![]() 邊上的黃金分割點(如圖2),則直線
邊上的黃金分割點(如圖2),則直線![]() 是
是![]() 的黃金分割線.你認為對嗎?為什么?
的黃金分割線.你認為對嗎?為什么?
(2)請你說明:三角形的中線是否也是該三角形的黃金分割線?
(3)研究小組在進一步探究中發(fā)現(xiàn):過點![]() 任作一條直線交
任作一條直線交![]() 于點
于點![]() ,再過點
,再過點![]() 作直線
作直線![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() (如圖3),則直線
(如圖3),則直線![]() 也是
也是![]() 的黃金分割線.
的黃金分割線.
請你說明理由.
(4)如圖4,點![]() 是
是![]() 的邊
的邊![]() 的黃金分割點,過點
的黃金分割點,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,顯然直線
,顯然直線![]() 是
是![]() 的黃金分割線.請你畫一條
的黃金分割線.請你畫一條![]() 的黃金分割線,使它不經(jīng)過
的黃金分割線,使它不經(jīng)過![]() 各邊黃金分割點.
各邊黃金分割點.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com