
【題目】如圖,已知點E、F在四邊形ABCD的對角線延長線上,AE=CF,DE∥BF,∠1=∠2. 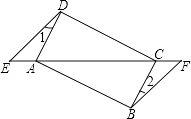
(1)求證:△AED≌△CFB;
(2)若AD⊥CD,四邊形ABCD是什么特殊四邊形?請說明理由.
【答案】
(1)證明:∵DE∥BF,
∴∠E=∠F,
在△AED和△CFB中,
 ,
,
∴△AED≌△CFB(AAS)
(2)解:四邊形ABCD是矩形.
理由如下:∵△AED≌△CFB,
∴AD=BC,∠DAE=∠BCF,
∴∠DAC=∠BCA,
∴AD∥BC,
∴四邊形ABCD是平行四邊形,
又∵AD⊥CD,
∴四邊形ABCD是矩形
【解析】(1)根據兩直線平行,內錯角相等可得∠E=∠F,再利用“角角邊”證明△AED和△CFB全等即可;(2)根據全等三角形對應邊相等可得AD=BC,∠DAE=∠BCF,再求出∠DAC=∠BCA,然后根據內錯角相等,兩直線平行可得AD∥BC,再根據一組對邊平行且相等的四邊形是平行四邊形證明四邊形ABCD是平行四邊形,再根據有一個角是直角的平行四邊形是矩形解答.


科目:初中數學 來源: 題型:
【題目】為增強學生的身體素質,教育行政部門規定學生每天參加戶外活動的平均時間不少于1小時.為了解學生參加戶外活動的情況,對部分學生參加戶外活動的時間進行抽樣調查,并將調查結果繪制作成如下兩幅不完整的統計圖,請你根據圖中提供的信息解答下列問題: 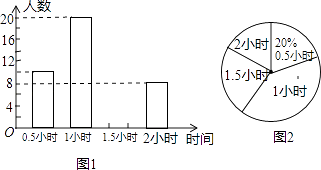
(1)一共調查了多少名學生;
(2)請補全條形統計圖;
(3)若該校共有6000名學生,根據以上調查結果估計該校全體學生每天參與戶外活動所用的總時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展以感恩教育為主題的藝術活動,舉辦了四個項目的比賽,它們分別是演講、唱歌、書法、繪畫.要求每位同學必須參加,且限報一項活動.以九年級(1)班為樣本進行統計,并將統計結果繪成如圖1、圖2所示的兩幅統計圖.請你結合圖示所給出的信息解答下列問題. 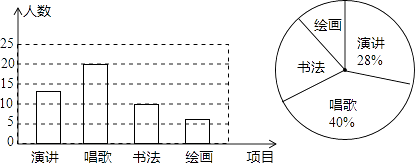
(1)求出參加繪畫比賽的學生人數占全班總人數的百分比?
(2)求出扇形統計圖中參加書法比賽的學生所在扇形圓心角的度數?
(3)若該校九年級學生有600人,請你估計這次藝術活動中,參加演講和唱歌的學生各有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 已知△ABC中,∠A=25°,∠B=40°. 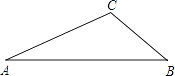
(1)求作:⊙O,使得⊙O經過A、C兩點,且圓心O落在AB邊上.(要求尺規作圖,保留作圖痕跡,不必寫作法)
(2)求證:BC是(1)中所作⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知過原點O的兩直線與圓心為M(0,4),半徑為2的圓相切,切點分別為P、Q,PQ交y軸于點K,拋物線經過P、Q兩點,頂點為N(0,6),且與x軸交于A、B兩點. 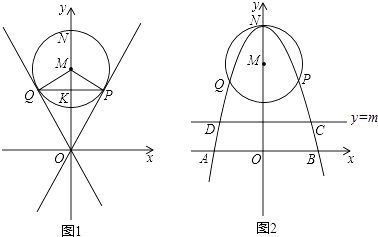
(1)求點P的坐標;
(2)求拋物線解析式;
(3)在直線y=nx+m中,當n=0,m≠0時,y=m是平行于x軸的直線,設直線y=m與拋物線相交于點C、D,當該直線與⊙M相切時,求點A、B、C、D圍成的多邊形的面積(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com