
【題目】如圖,在矩形OABC中,AO=10,AB=8,沿直線CD折疊矩形OABC的一邊BC,使點B落在OA邊上的點E處.分別以OC,OA所在的直線為x軸,y軸建立平面直角坐標系,拋物線y=ax2+bx+c經過O,D,C三點.
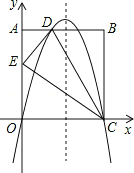
(1)求AD的長及拋物線的解析式;
(2)一動點P從點E出發,沿EC以每秒2個單位長的速度向點C運動,同時動點Q從點C出發,沿CO以每秒1個單位長的速度向點O運動,當點P運動到點C時,兩點同時停止運動.設運動時間為t秒,當t為何值時,以P、Q、C為頂點的三角形與△ADE相似?
(3)點N在拋物線對稱軸上,點M在拋物線上,是否存在這樣的點M與點N,使以M,N,C,E為頂點的四邊形是平行四邊形?若存在,請直接寫出點M與點N的坐標(不寫求解過程);若不存在,請說明理由.
【答案】(1)AD=3,![]() (2)當
(2)當![]() 或
或![]() 時,以P、Q、C為頂點的三角形與△ADE相似(3)存在符合條件的M、N點,它們的坐標為:①M1(﹣4,﹣32),N1(4,﹣38);
時,以P、Q、C為頂點的三角形與△ADE相似(3)存在符合條件的M、N點,它們的坐標為:①M1(﹣4,﹣32),N1(4,﹣38);
②M2(12,﹣32),N2(4,﹣26);③M3(4,![]() ),N3(4,﹣
),N3(4,﹣![]() )
)
【解析】
解:(1)∵四邊形ABCO為矩形,∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10。
由折疊的性質得,△BDC≌△EDC,∴∠B=∠DEC=90°,EC=BC=10,ED=BD。
由勾股定理易得EO=6。∴AE=10﹣6=4。
設AD=x,則BD=CD=8﹣x,由勾股定理,得x2+42=(8﹣x)2,解得,x=3。
∴AD=3。
∵拋物線y=ax2+bx+c過點D(3,10),C(8,0),
∴![]() ,解得
,解得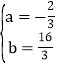 。∴拋物線的解析式為:
。∴拋物線的解析式為:![]() 。
。
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,∴∠DEA=∠OCE,
由(1)可得AD=3,AE=4,DE=5。而CQ=t,EP=2t,∴PC=10﹣2t。
當∠PQC=∠DAE=90°,△ADE∽△QPC,
∴![]() ,即
,即![]() ,解得
,解得![]() 。
。
當∠QPC=∠DAE=90°,△ADE∽△PQC,
∴![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴當![]() 或
或![]() 時,以P、Q、C為頂點的三角形與△ADE相似。
時,以P、Q、C為頂點的三角形與△ADE相似。
(3)存在符合條件的M、N點,它們的坐標為:①M1(﹣4,﹣32),N1(4,﹣38);
②M2(12,﹣32),N2(4,﹣26);③M3(4,![]() ),N3(4,﹣
),N3(4,﹣![]() )。
)。
(1)根據折疊圖形的軸對稱性,△CED≌△CBD,在Rt△CEO中求出OE的長,從而可得到AE的長;在Rt△AED中,AD=AB﹣BD、ED=BD,利用勾股定理可求出AD的長.進一步能確定D點坐標,利用待定系數法即可求出拋物線的解析式。
(2)由于∠DEC=90°,首先能確定的是∠AED=∠OCE,若以P、Q、C為頂點的三角形與△ADE相似,那么∠QPC=90°或∠PQC=90°,然后在這兩種情況下,分別利用相似三角形的對應邊成比例求出對應的t的值。
(3)假設存在符合條件的M、N點,分兩種情況討論:
①EC為平行四邊形的對角線,由于拋物線的對稱軸經過EC中點,若四邊形MENC是平行四邊形,那么M點必為拋物線頂點。
由![]() 得拋物線頂點,則:M(4,
得拋物線頂點,則:M(4,![]() )。
)。
∵平行四邊形的對角線互相平分,∴線段MN必被EC中點(4,3)平分,則N(4,﹣![]() )。
)。
②EC為平行四邊形的邊,則EC![]() MN,
MN,
設N(4,m),則M(4﹣8,m+6)或M(4+8,m﹣6);
將M(﹣4,m+6)代入拋物線的解析式中,得:m=﹣38,
此時 N(4,﹣38)、M(﹣4,﹣32);
將M(12,m﹣6)代入拋物線的解析式中,得:m=﹣26,
此時 N(4,﹣26)、M(12,﹣32)。
綜上所述,存在符合條件的M、N點,它們的坐標為:①M1(﹣4,﹣32),N1(4,﹣38);
②M2(12,﹣32),N2(4,﹣26);③M3(4,![]() ),N3(4,﹣
),N3(4,﹣![]() )。
)。


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:初中數學 來源: 題型:
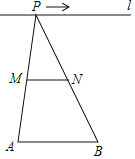
【題目】如圖,已知線段![]() ,
,![]() 是直線
是直線![]() 上一動點,點
上一動點,點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,對下列各值:①線段
的中點,對下列各值:①線段![]() 的長;②
的長;②![]() 的周長;③
的周長;③![]() 的面積;④直線
的面積;④直線![]() ,
,![]() 之間的距離;⑤
之間的距離;⑤![]() 的大小.其中不會隨點
的大小.其中不會隨點![]() 的移動而改變的是_____.(填序號)
的移動而改變的是_____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 是對角線
是對角線![]() 上一個動點,連結
上一個動點,連結![]() ,過
,過![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分別為垂足.
分別為垂足.
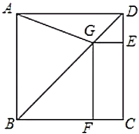
(1)求證:![]() ;
;
(2)①寫出![]() 、
、![]() 、
、![]() 三條線段滿足的等量關系,并證明;②求當
三條線段滿足的等量關系,并證明;②求當![]() ,
,![]() 時,
時,![]() 的長
的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人分別加工100個零件,甲第1個小時加工了10個零件,之后每小時加工30個零件.乙在甲加工前已經加工了40個零件,在甲加工3小時后乙開始追趕甲,結果兩人同時完成任務.設甲、乙兩人各自加工的零件數為![]() (個),甲加工零件的時間為
(個),甲加工零件的時間為![]() (時),
(時),![]() 與
與![]() 之間的函數圖象如圖所示.
之間的函數圖象如圖所示.

(1)在乙追趕甲的過程中,求乙每小時加工零件的個數.
(2)求甲提高加工速度后甲加工的零件數![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(3)當甲、乙兩人相差12個零件時,直接寫出甲加工零件的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
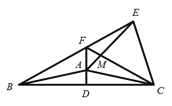
【題目】已知:如圖,在等腰三角形ABC中,120BAC180,ABAC,ADBC于點D,以AC為邊作等邊三角形ACE,ACE與ABC在直線AC的異側,直線BE交直線AD于點F,連接FC交AE于點M.
(1)求EFC的度數;
(2)求證:FE+FA=FC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】徐州至北京的高鐵里程約為700km,甲、乙兩人從徐州出發,分別乘坐“徐州號”高鐵A與“復興號”高鐵B前往北京.已知A車的平均速度比B車的平均速度慢80km/h,A車的行駛時間比B車的行駛時間多40%,兩車的行駛時間分別為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,∠ABD、∠CDB的平分線BE、DF分別交邊AD、BC于點E、F.
(1)求證:四邊形BEDF是平行四邊形;
(2)當∠ABE為多少度時,四邊形BEDF是菱形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在菱形![]() 中,
中,![]() ,點
,點![]() 是射線
是射線![]() 上一動點,以
上一動點,以![]() 為邊向右側作等邊
為邊向右側作等邊![]() ,點
,點![]() 的位置隨著點
的位置隨著點![]() 的位置變化而變化.
的位置變化而變化.
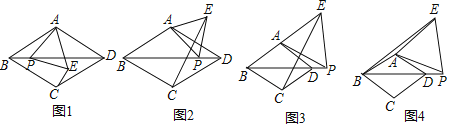
(1)如圖1,當點![]() 在菱形
在菱形![]() 內部或邊上時,連接
內部或邊上時,連接![]() ,
,![]() 與
與![]() 的數量關系是______,
的數量關系是______,![]() 與
與![]() 的位置關系是______;
的位置關系是______;
(2)當點![]() 在菱形
在菱形![]() 外部時,(1)中的結論是否還成立?若成立,請予以證明;若不成立,請說明理由(選擇圖2,圖3中的一種情況予以證明或說理);
外部時,(1)中的結論是否還成立?若成立,請予以證明;若不成立,請說明理由(選擇圖2,圖3中的一種情況予以證明或說理);
(3)如圖4,當點![]() 在線段
在線段![]() 的延長線上時,連接
的延長線上時,連接![]() ,若
,若![]() ,
,![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com