【題目】經市場調研發現：某品牌童裝平均每天可售出 20 件，每件盈利 40元．在每件降價幅度不超過 18 元的情況下，若每件童裝降價 1 元，則每天可多售出 2 件，設降價 x 元．
（1）降價 x 元后，每件童裝盈利是多少元，每天銷售量是多少件；
（2）要想每天銷售這種童裝盈利 1200 元，那么每件童裝應降價多少元？
（3）每天能盈利 1800 元嗎？如果能，每件童裝應降價多少元？如果不能，請說明理由．
【答案】（1）降價 x 元后，每件童裝盈利是（40﹣x）元，每天銷售量是（20+2x）件；（2）每件童裝降價 10 元；（3）不能，理由見解析.
【解析】
（1）根據每件童裝降價 1 元，每天可多售出 2 件，即可表示出每天的銷售數量,
（2）根據總利潤=單件利潤
銷售數量,列出一元二次方程,求解即可,
（3）列方程表示出根的判別式即可解題.
（1）降價 x 元后，每件童裝盈利是（40﹣x）元，每天銷售量是（20+2x）件；
（2）依題意得：（40﹣x）（20+2x）＝1200，解得：x1＝10，x2＝20（舍去），
答：每件童裝降價 10 元；
（3）不能，理由如下：
依題意得：（40﹣x）（20+2x）＝1800，即：x2﹣30x+500＝0，
∵△＝302﹣4×1×500＝900﹣2000＝﹣1100＜0，
∴原方程無解，
∴每天銷售這種童裝不可能盈利 1800 元．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】為了了解某市120000名初中學生的視力情況，某校數學興趣小組，并進行整理分析．
（1）小明在眼鏡店調查了1000名初中學生的視力，小剛在鄰居中調查了20名初中學生的視力，他們的抽樣是否合理？并說明理由．
（2）該校數學興趣小組從該市七、八、九年級各隨機抽取了1000名學生進行調查，整理他們的視力情況數據，得到如下的折線統計圖．
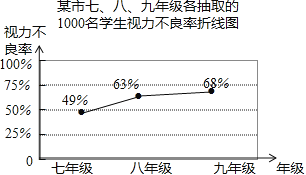
請你根據抽樣調查的結果，估計該市120000名初中學生視力不良的人數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，方格紙中每個小正方形的邊長都是1個單位長度，Rt△ABC的三個頂點A(-2，2)，B(0，5)，C(0，2).
(1)將△ABC以點C為旋轉中心旋轉180°，得到△A1B1C，請畫出△A1B1C的圖形.
(2)平移△ABC，使點A的對應點A2坐標為(-2，-6)，請畫出平移后對應的△A2B2C2的圖形.
(3)若將△A1B1C繞某一點旋轉可得到△A2B2C2，請直接寫出旋轉中心的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形ABCD中，E是邊CD上一點（點E不與點C、D重合），連結BE．
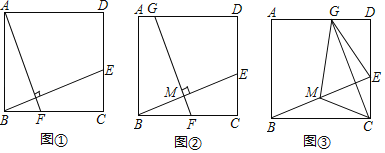
（感知）如圖①，過點A作AF⊥BE交BC于點F．易證△ABF≌△BCE．（不需要證明）
（探究）如圖②，取BE的中點M，過點M作FG⊥BE交BC于點F，交AD于點G．
（1）求證：BE=FG．
（2）連結CM，若CM=1，則FG的長為 ．
（應用）如圖③，取BE的中點M，連結CM．過點C作CG⊥BE交AD于點G，連結EG、MG．若CM=3，則四邊形GMCE的面積為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
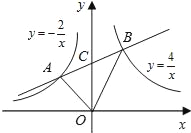
【題目】如圖，點A是反比例函數
在第二象限內圖象上一點，點B是反比例函
數在第一象限內圖象上一點，直線AB與y軸交于點C，且AC=BC，連接OA、OB，求△AOB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】李大爺按每千克2.1元批發了一批黃瓜到鎮上出售，為了方便，他帶了一些零錢備用．他先按市場售出一些后，又降低出售．售出黃瓜千克數x與他手中持有的錢數y元（含備用零錢）的關系如圖所示，結合圖象回答下列問題：
（1）李大爺自帶的零錢是多少？
（2）降價前他每千克黃瓜出售的價格是多少？
（3）賣了幾天，黃瓜賣相不好了，隨后他按每千克下降1.6元將剩余的黃瓜售完，這時他手中的錢（含備用的錢）是530元，問他一共批發了多少千克的黃瓜？
（4）請問李大爺虧了還是賺了？若虧（賺）了，虧（賺）多少錢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列方程的解法中，錯誤的個數是（ ）
①方程2x-1=x+1移項，得3x=0
②方程
=1去分母，得x-1=3=x=4
③方程1-
去分母，得4-x-2=2（x-1）
④方程
去分母，得2x-2+10-5x=1
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面推理過程：
如圖，∠1＋∠2＝230°，b∥c，則∠1，∠2，∠3，∠4各是多少度？
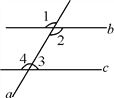
解：∵∠1＝∠2(__________________)，
∠1＋∠2＝230°，
∴∠1＝∠2＝___________(填度數)．
∵b∥c，
∴∠4＝∠2＝_______(填度數)(_______________________________)，
∠2＋∠3＝180°(________________________________)，
∴∠3＝180°－∠2＝____________(填度數)．
查看答案和解析>>
科目：初中數學 來源： 題型：
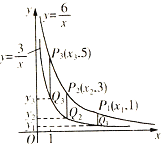
【題目】兩個反比例函數
,
在第一象限內的圖象如圖所示，點P1，P2，P3，……P2005在反比例函數圖象上，它們的橫坐標分別是x1，x2，x3，x2005縱坐標分別為1，3，5，……；
共2005個連續奇數，過點P1，P2，P3，……，P2005分別作
軸的平行線，與的圖象交點依次是Q1(x1，y1)，Q2（x2，y2），Q3(x3,y3)，……，Q2005（x2005，y2005）,則
_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com