
如圖,在等腰直角三角板ABC中,斜邊BC為2個單位長度,現把這塊三角板在平面直角坐標系xOy中滑動,并使B、C兩點始終分別位于y軸、x軸的正半軸上,直角頂點A與原點O位于BC兩側.
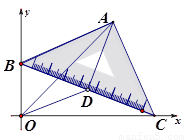
(1)取BC中點D,問OD+DA的長度是否發生改變,若會,說明理由;若不會,求出OD+DA長度;
(2)你認為OA的長度是否會發生變化?若變化,那么OA最長是多少?OA最長時四邊形OBAC是怎樣的四邊形?并說明理由;
(3)填空:當OA最長時A的坐標是( , ),直線OA的解析式是 .
(1)2;(2)2,正方形,理由見解析;(3)y=x.
【解析】
試題分析:(1)根據直角三角形的斜邊上的中線等于斜邊的一半,即可得到OD=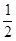 BC=2×
BC=2×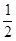 =1,則不隨三角板的移動而改變,因而OD+DA不會改變;
=1,則不隨三角板的移動而改變,因而OD+DA不會改變;
(2)根據兩點之間線段最短,即可得到當O、D、A三點在一直線上時,OA最長,即可求解;
(3)當O、D、A三點在一直線上時,OA最長,且此時OA是第一象限的角平分線,據此即可求解.
試題解析:
解:(1)OD=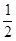 BC=2×
BC=2×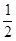 =1,則OD+DA=2.
=1,則OD+DA=2.
(2)∵OD=DA=1始終不變,
∴當O、D、A三點在一直線上時,OA最長等于2.
這時,四邊形OBAC的對角線相交于點D,有DO=DB=DA=DC=1,OA=BC=2,
∵四邊形OBAC是矩形,
又∵AB=AC,
∴四邊形OBAC是正方形.
(3)A(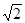 ,
,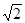 )
)
直線OA是∠BOC的角平分線,則解析式是:y=x.
考點:1.一次函數綜合題;2.等腰直角三角形3.矩形的性質及正方形的判定.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:
| 底邊 |
| 腰 |
| BC |
| AB |
 互唯一確定的.
互唯一確定的.| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A=.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:

(1)sad 的值為( ▼ )
A. B.1 C.
D.2
(2)對于,∠A的正對值sad A的取值范圍是 ▼ .
(3)已知,其中
為銳角,試求sad
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
 .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
 的值為( ▼ )
的值為( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ . ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.查看答案和解析>>
科目:初中數學 來源:2011屆北京市昌平區初三上學期期末考試數學卷 題型:解答題
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A= .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:
(1)sad  的值為( ▼ )
的值為( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ . ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.查看答案和解析>>
科目:初中數學 來源:2010-2011學年北京市昌平區初三上學期期末考試數學卷 題型:解答題
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A= .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:

(1)sad  的值為( ▼ )
的值為( ▼ )
A.  B.
1 C.
B.
1 C.  D.
2
D.
2
(2)對于 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ .
(3)已知 ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com