
【題目】“校園安全”受到全社會的廣泛關注,綿陽市某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了如圖兩幅尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題: 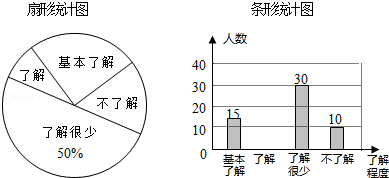
(1)接受問卷調查的學生共有人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為;
(2)請補全條形統計圖;
(3)若該中學共有學生3000人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數;
(4)若從對校園安全知識達到了“了解”程度的3個女生和2個男生中隨機抽取2人參加校園安全知識競賽,請用樹狀圖或列表法求出恰好抽到1個男生和1個女生的概率.
【答案】
(1)60;90°
(2)解:60﹣15﹣30﹣10=5;
補全條形統計圖得:

(3)解:根據題意得:3000× ![]() =1000(人),
=1000(人),
則估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數為1000人
(4)解:畫樹狀圖得:

∵共有20種等可能的結果,恰好抽到1個男生和1個女生的有12種情況,
∴恰好抽到1個男生和1個女生的概率為: ![]() =
= ![]()
【解析】解:(1)∵了解很少的有30人,占50%, ∴接受問卷調查的學生共有:30÷50%=60(人);
∴扇形統計圖中“基本了解”部分所對應扇形的圓心角為: ![]() ×360°=90°;
×360°=90°;
所以答案是:60,90°;
【考點精析】解答此題的關鍵在于理解扇形統計圖的相關知識,掌握能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況,以及對條形統計圖的理解,了解能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況.


科目:初中數學 來源: 題型:
【題目】甲、乙兩校派相同人數的優秀學生,參加縣教育局舉辦的中小學生美文誦讀決賽。比賽結束后,發現學生成績分別是7分、8分、9分或10分(滿分10分),核分員依據統計數據繪制了如下尚不完整的統計圖表。根據這些材料,請你回答下列問題:
甲校成績統計表 | ||||
成績 | 7分 | 8分 | 9分 | 10分 |
人數 | 11 | 0 | 8 | |
(1)在圖①中,“7分”所在扇形的圓心角等于_______
(2)求圖②中,“8分”的人數,并請你將該統計圖補充完整。


(3)經計算,乙校學生成績的平均數是8.3分,中位數是8分。請你計算甲校學生成績的平均數、中位數,并從平均數和中位數的角度分析哪個學校的成績較好?
(4)如果教育局要組織8人的代表隊參加市級團體賽,為便于管理,決定從這兩所學校中的一所挑選參賽選手,請你分析,應選哪所學校?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據解答過程填空(理由或數學式)
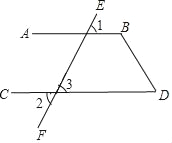
如圖,已知∠1=∠2,∠D=60°,求∠B的度數.
解∵∠2=∠3( )
又∵∠1=∠2(已知),
∴∠3=∠1(等量代換)
∴ ∥ ( )
∴∠D+∠B=180°( )
又∵∠D=60°(已知),
∴∠B= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰△ABC中,當頂角A的大小確定時,它的對邊BC與鄰邊(腰AB或AC)的比值確定,記為f(A),易得f(60°)=1.若α是等腰三角形的頂角,則f(α)的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,E在AB上,且∠DCE=67.5°,DE⊥AB于E,若AE=1,線段BE的長為____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A,B分別為數軸上的兩點,點A表示的數是﹣30,點B表示的數是50.
![]()
(1)請寫出線段AB中點M表示的數是 .
(2)現有一只螞蟻P從點B出發,以每秒3個單位長度的速度沿數軸向左移動,同時另一只螞蟻Q恰好從點A出發,以每秒2個單位長度的速度沿數軸向右移動,設兩只螞蟻在數軸上的點C相遇.
①求A、B兩點間的距離;
②求兩只螞蟻在數軸上的點C相遇時所用的時間;
③求點C對應的數是多少?
(3)若螞蟻P從點B出發,以每秒3個單位長度的速度沿數軸向左運動,同時另一只螞蟻恰好從A點出發,以每秒2個單位長度的速度沿數軸也向左運動,設兩只螞蟻在數軸上的D點相遇,求D點表示的數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,兩個形狀、大小完全相同的含有30゜和60゜的三角板如圖放置,PA、PB與直線MN重合,且三角板PAC,三角板PBD均可以繞點P逆時針旋轉.
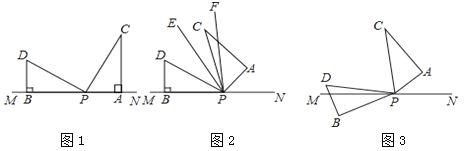
(1)試說明:∠DPC=90゜;
(2)如圖2,若三角板PAC的邊PA從PN處開始繞點P逆時針旋轉一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
(3)如圖3,若三角板PAC的邊PA從PN處開始繞點P逆時針旋轉,轉速為3゜/秒,同時三角板PBD的邊PB從PM處開始繞點P逆時針旋轉,轉速為2゜/秒,在兩個三角板旋轉過程中(PC轉到與PM重合時,兩三角板都停止轉動),以下兩個結論:①![]() 為定值;②∠BPN+∠CPD為定值,請選出正確的結論,并說明理由.
為定值;②∠BPN+∠CPD為定值,請選出正確的結論,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分9分)小明從家騎自行車出發,沿一條直路到相距2400m的郵局辦事,小明出發
的同時,他的爸爸以96m/min速度從郵局同一條道路步行回家,小明在郵局停留2min后沿原路
以原速返回,設他們出發后經過t min時,小明與家之間的距離為s1 m,小明爸爸與家之間的距
離為s2 m,圖中折線OABD、線段EF分別表示s1、s2與t之間的函數關系的圖象.
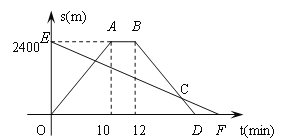
(1)求s2與t之間的函數關系式;
(2)小明從家出發,經過多長時間在返回途中追上爸爸?這時他們距離家還有多遠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com