
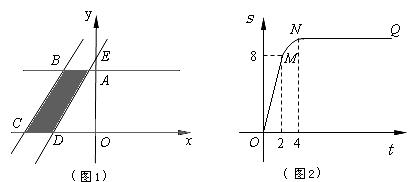
如圖1所示,直角梯形OABC的頂點A、C分別在y軸正半軸與![]() 軸負半軸上.過點B、C作直線
軸負半軸上.過點B、C作直線![]() .將直線
.將直線![]() 平移,平移后的直線
平移,平移后的直線![]() 與
與![]() 軸交于點D,與
軸交于點D,與![]() 軸交于點E.
軸交于點E.
(1)將直線![]() 向右平移,設平移距離CD為
向右平移,設平移距離CD為![]() (t
(t![]() 0),直角梯形OABC被直線
0),直角梯形OABC被直線![]() 掃過的面積(圖中陰影部份)為
掃過的面積(圖中陰影部份)為![]() ,
,![]() 關于
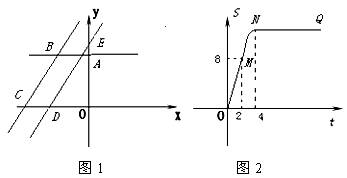
關于![]() 的函數圖象如圖2所示, OM為線段,MN為拋物線的一部分,NQ為射線,N點橫坐標為4.
的函數圖象如圖2所示, OM為線段,MN為拋物線的一部分,NQ為射線,N點橫坐標為4.
①求梯形上底AB的長及直角梯形OABC的面積;
②當![]() 時,求S關于
時,求S關于![]() 的函數解析式;
的函數解析式;
(2)在第(1)題的條件下,當直線![]() 向左或向右平移時(包括
向左或向右平移時(包括![]() 與直線BC重合),在直線AB上是否存在點P,使
與直線BC重合),在直線AB上是否存在點P,使![]() 為等腰直角三角形?若存在,請直接寫出所有滿足條件的點P的坐標;若不存在,請說明理由.
為等腰直角三角形?若存在,請直接寫出所有滿足條件的點P的坐標;若不存在,請說明理由.
解:
(1)①![]()
![]() ,
,![]() ,S梯形OABC=12
,S梯形OABC=12
②當![]() 時,
時,
直角梯形OABC被直線![]() 掃過的面積=直角梯形OABC面積-直角三角開DOE面積
掃過的面積=直角梯形OABC面積-直角三角開DOE面積
![]()
(2) 存在
![]()
解法二:
① 以點D為直角頂點,作![]() 軸
軸
![]()
![]() 設
設![]() .
.![]() (圖示陰影)
(圖示陰影)
![]()
![]()
![]() ,在上面二圖中分別可得到
,在上面二圖中分別可得到![]() 點的生標為P(-12,4)、P(-4,4)
點的生標為P(-12,4)、P(-4,4)
E點在0點與A點之間不可能;
② 以點E為直角頂點
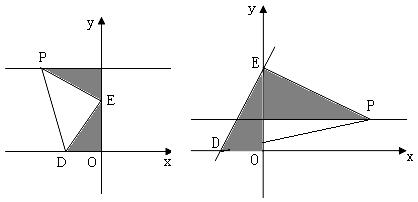
同理在②二圖中分別可得![]() 點的生標為P(-
點的生標為P(-![]() ,4)、P(8,4)E點在0點下方不可能.
,4)、P(8,4)E點在0點下方不可能.
③ 以點P為直角頂點
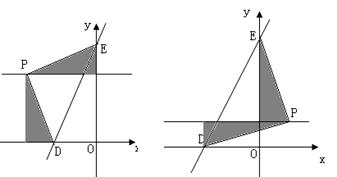
同理在③二圖中分別可得![]() 點的生標為P(-4,4)(與①情形二重合舍去)、P(4,4),
點的生標為P(-4,4)(與①情形二重合舍去)、P(4,4),
E點在A點下方不可能.
綜上可得![]() 點的坐標共5個解,分別為P(-12,4)、P(-4,4)、P(-
點的坐標共5個解,分別為P(-12,4)、P(-4,4)、P(-![]() ,4)、
,4)、
P(8,4)、P(4,4).
下面提供參考解法三:
以直角進行分類進行討論(分三類):
第一類如上解法⑴中所示圖![]()
![]()
![]()
![]() ,直線
,直線![]() 的中垂線方程:
的中垂線方程:![]() ,令
,令![]() 得
得![]() .由已知可得
.由已知可得![]() 即
即![]() 化簡得
化簡得![]() 解得
解得 ![]()
![]() ;
;
第二類如上解法②中所示圖![]()
![]() ,
,
直線![]() 的方程:
的方程:![]() ,令
,令![]() 得
得![]() .
.
由已知可得![]() 即
即![]() 化簡得
化簡得![]() 解之得 ,
解之得 ,![]()
![]()
第三類如上解法③中所示圖![]()
![]()
,直線![]() 的方程:
的方程:![]() ,令
,令![]() 得
得![]() .由已知可得
.由已知可得![]() 即
即![]() 解得
解得![]()
![]() (
(![]() 與
與![]() 重合舍去).
重合舍去).
綜上可得![]() 點的坐標共5個解,分別為P(-12,4)、P(-4,4)、P(-
點的坐標共5個解,分別為P(-12,4)、P(-4,4)、P(-![]() ,4)、
,4)、
P(8,4)、P(4,4).
事實上,我們可以得到更一般的結論:
如果得出![]()
![]() 設
設![]() ,則P點的情形如下
,則P點的情形如下
| 直角分類情形 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
|
|


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》常考題集(23):2.8 二次函數的應用(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第20章《二次函數和反比例函數》常考題集(22):20.5 二次函數的一些應用(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2010年浙江省杭州市蕭山區中考數學模擬試卷36(義橋實驗學校 嚴炯炯)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com