
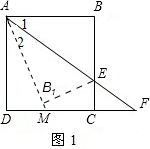
 =x”,其它條件都不變,試寫出△ABE翻折后與正方形ABCD公共部分的面積y與x的關系式及自變量x的取值范圍(只要寫出結論,不需寫出解題過程).
=x”,其它條件都不變,試寫出△ABE翻折后與正方形ABCD公共部分的面積y與x的關系式及自變量x的取值范圍(只要寫出結論,不需寫出解題過程).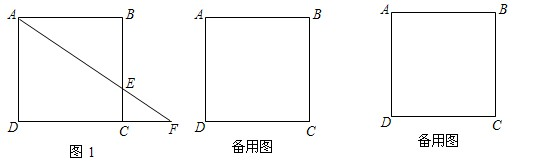
 =
= ,
, =
= ,
, ;
;
 -x,
-x, -x)2,
-x)2, ,
, ,AM=
,AM= ,
, =
= ;
;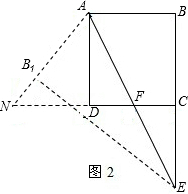
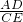 =
= ,
, ,
, .
. )2,
)2, .
. ,AN=
,AN= sin∠DAB1=
sin∠DAB1= =
= ;
;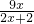 ,定義域為x>0;
,定義域為x>0;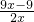 ,定義域為x>1.
,定義域為x>1.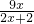 ,定義域為x>0;若點E在邊BC的延長線上,y=
,定義域為x>0;若點E在邊BC的延長線上,y=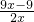 ,定義域為x>1.
,定義域為x>1.

科目:初中數學 來源: 題型:
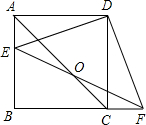 CF.
CF.| 1 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
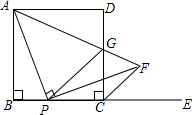 如圖,已知邊長為2的正方形ABCD,P是BC邊上一點,E是BC邊延長線上一點,過點P作PF⊥AP與∠DCE的平分線CF交于點F.AF與CD交于點G.
如圖,已知邊長為2的正方形ABCD,P是BC邊上一點,E是BC邊延長線上一點,過點P作PF⊥AP與∠DCE的平分線CF交于點F.AF與CD交于點G.查看答案和解析>>
科目:初中數學 來源: 題型:
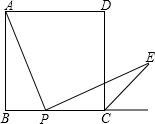 (2013•桂林)如圖,已知邊長為4的正方形ABCD,P是BC邊上一動點(與B、C不重合),連結AP,作PE⊥AP交∠BCD的外角平分線于E.設BP=x,△PCE面積為y,則y與x的函數關系式是( )
(2013•桂林)如圖,已知邊長為4的正方形ABCD,P是BC邊上一動點(與B、C不重合),連結AP,作PE⊥AP交∠BCD的外角平分線于E.設BP=x,△PCE面積為y,則y與x的函數關系式是( )
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
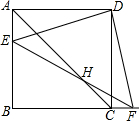 如圖,已知邊長為4的正方形ABCD,點E在AB上,點F在BC的延長線上,EF與AC交于點H,且AE=CF=m,則四邊形EBFD的面積為
如圖,已知邊長為4的正方形ABCD,點E在AB上,點F在BC的延長線上,EF與AC交于點H,且AE=CF=m,則四邊形EBFD的面積為查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com