
 ),C(2,0),固定正方形ABCD,直線L經過AC兩點;將正方形CEFG繞點C順時針旋轉135°得到正方形CE1F1G1,
),C(2,0),固定正方形ABCD,直線L經過AC兩點;將正方形CEFG繞點C順時針旋轉135°得到正方形CE1F1G1,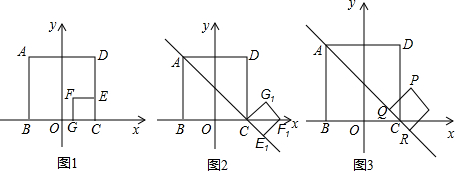
 ,那么其對角線CF長度為2,
,那么其對角線CF長度為2, 時,S=
時,S= t2;
t2; <t≤
<t≤ 時,S=-
時,S=- t2+2
t2+2 t-2;
t-2; <t≤3
<t≤3 時,S=2;
時,S=2; <t≤4
<t≤4 時 S=-
時 S=- t2+3
t2+3 t-7;
t-7; <t≤5
<t≤5 時,S=
時,S= t2-5
t2-5 t+25;
t+25; 時,解
時,解 t2=1,解得:t=
t2=1,解得:t= ;
; <t≤
<t≤ 時,解2-
時,解2- (2
(2 -t)2=1,解得:t=
-t)2=1,解得:t= 或3
或3 ,(舍去);
,(舍去); <t≤
<t≤ 時,解
時,解 (4
(4 -t)2=1,解得:t=3
-t)2=1,解得:t=3 或5
或5 (5
(5 不合題意,舍去).
不合題意,舍去). 或3
或3 .
. 時,那么P位于CD中點處,P的坐標是:(2,2),設直線m的解析式是y=kx+b,
時,那么P位于CD中點處,P的坐標是:(2,2),設直線m的解析式是y=kx+b,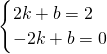 ,
,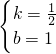
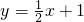 ,
,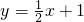 中,令y=a,解得:x=2(a-1),則M的橫坐標是2(a-1);
中,令y=a,解得:x=2(a-1),則M的橫坐標是2(a-1); ,
, 代入
代入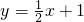 中,解得:x=
中,解得:x= .
.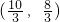 .
. 時,P是AD與y軸的交點,則P的坐標是:(0,4).
時,P是AD與y軸的交點,則P的坐標是:(0,4). ,
,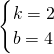 ,
, (a-4),則M的橫坐標是
(a-4),則M的橫坐標是 (a-1);
(a-1); (a-4)-(2-a)=4,解得:a=
(a-4)-(2-a)=4,解得:a= ,
, 代入y=2x+4中,解得x=-
代入y=2x+4中,解得x=- .
. ,
, ).
). ,
, )或(-
)或(- ,
, )
) 的正方形,則△CE1F1是等腰直角三角形,直角邊長是
的正方形,則△CE1F1是等腰直角三角形,直角邊長是 ,則E1的坐標即可求解,E1與AC在一條直線上;
,則E1的坐標即可求解,E1與AC在一條直線上; ,當
,當 <t≤
<t≤ ,
, <t≤3
<t≤3 ,3
,3 <t≤
<t≤ ,4
,4 <t≤5
<t≤5 五種情況利用三角形的面積公式即可求解;
五種情況利用三角形的面積公式即可求解;

 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:初中數學 來源: 題型:
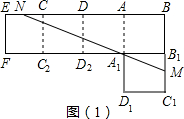
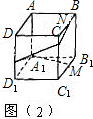
| 1 |
| MB |
| 1 |
| NB |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |

查看答案和解析>>
科目:初中數學 來源:數學教研室 題型:044
如圖,甲、乙兩個正方形紙片部分重疊在一起.已知重疊部分(陰影)面積與甲正方形面積之比是4∶21,重疊部分與乙正方形面積之比是3∶7.且甲正方形除陰影部分之外的面積是 ,則乙正方形的面積是多少平方厘米?
,則乙正方形的面積是多少平方厘米?
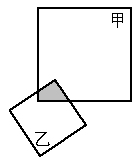
查看答案和解析>>
科目:初中數學 來源:黑龍江省期末題 題型:解答題
 ),C(2,0),固定正方形ABCD,直線L經過AC兩點;將正方形CEFG繞點C順時針旋轉135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直線L經過AC兩點;將正方形CEFG繞點C順時針旋轉135°得到正方形CE1F1G1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com