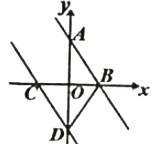
【題目】如圖，已知一條直線經過點A（0，2）、點B（1，0），將這條直線向左平移與x軸、y軸分別交與點C、點D.若DB=DC，則直線CD的函數解析式為_____
科目：初中數學 來源： 題型：
【題目】如圖所示，∠AOB是平角，OM、ON分別是∠AOC、∠BOD的平分線．
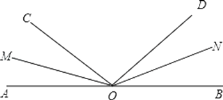
（1）當∠BOC=140°時，求∠AOM的度數；
（2）當∠AOC=30°，∠BOD=60°時，求∠MON的度數；
（3）當∠COD=x度時，則∠MON=________度.（請直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，點E在邊AD上，將此矩形沿CE折疊，點D落在點F處，連接BF，B、F、E三點恰好在一直線上．
（1）求證：△BEC為等腰三角形；（2）若AB＝2，∠ABE＝45°，求矩形ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，A．B兩地之間有一條河，原來從A地到B地需要經過橋DC，沿折線A→D→C→B到達B地，現在新建了橋EF，可直接沿直線AB從A地到達B地．BC=1000m，∠A=45°，∠B=37°．橋DC和AB平行，則現在從A地到達B地可比原來少走多少路程？（結果精確到1m．參考數據：
，sin37°≈0.60，cos37°≈0.80）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】騎共享單車已成為人們喜愛的一種綠色出行方式．已知A、B、C三家公司的共享單車都是按騎車時間收費，標準如下：
公司 | 單價（元/半小時） | 充值優惠 |
A | m | 充20元送5元，即：充20元實得25元 |
B | m－0.2 | 無 |
C | 1 | 充20元送20元，即：充20元實得40元 |
（注：使用這三家公司的共享單車，不足半小時均按半小時計費．用戶的賬戶余額長期有效，但不可提現．）
4月初，李明注冊成了A公司的用戶，張紅注冊成了B公司的用戶，并且兩人在各自賬戶上分別充值20元．一個月下來，李明、張紅兩人使用單車的次數恰好相同，且每次都在半小時以內，結果到月底李明、張紅的賬戶余額分別顯示為5元、8元．
（1）求m的值；
（2）5月份，C公司在原標準的基礎上又推出新優惠：每月的月初給用戶送出5張免費使用券（1
次用車只能使用1張券）．如果王磊每月使用單車的次數相同，且在30次以內，每次用車都不超過
半小時. 若要在這三家公司中選擇一家并充值20元，僅從資費角度考慮，請你幫他作出選擇，并說
明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC是等邊三角形，點D、E分別在BC、AC上，且BD=CE，AD與BE相交于點F．
（1）試說明△ABD≌△BCE；
（2）△EAF與△EBA相似嗎？說說你的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司購買了一批
、
型芯片，其中型芯片的單價比型芯片的單價少9元，已知該公司用3120元購買型芯片的條數與用4200元購買型芯片的條數相等．
（1）求該公司購買的、型芯片的單價各是多少元？
（2）若兩種芯片共購買了200條，且購買的總費用為6280元，求購買了多少條型芯片？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(1)一個兩位數A,十位數字為a,個位數字為b,交換a和b的位置,得到一個新的兩位數B,則A+B一定能被______整除,A-B一定能被______整除；
(2)一個三位數M,百位數字為a,十位數字為b,個位數字為c（a，b，c均為1至9的整數）,交換a和c的位置,得到一個新的三位數N.請用含a、b、c的式子分別表示數N與M-N；
(3) 若(2)中a比b大1,M比N大792，求M.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某工廠計劃生產
兩種產品共60件，需購買甲、乙兩種材料.生產一件
產品需甲種材料4千克；生產一件
產品需甲、乙兩種材料各3千克.經測算，購買甲、乙兩種材料各1千克共需資金60元；購買甲種材料2千克和乙種材料3千克共需資金155元.
（1）甲、乙兩種材料每千克分別是多少元？
（2）現工廠用于購買甲、乙兩種材料的資金不超過9900元，且生產產品不少于38件，問符合生產條件的生產方案有哪幾種？
（3）在（2）的條件下，若生產一件產品需加工費40元，生產一件產品需加工費50元，應選擇哪種生產方案，使生產這60件產品的成本最低（成本=材料費+加工費）？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
