
如圖,拋物線 的對稱軸是直線x=
的對稱軸是直線x= ,與x軸交于點A、B兩點,與y軸交于點C,并且點A的坐標為(—1,0).
,與x軸交于點A、B兩點,與y軸交于點C,并且點A的坐標為(—1,0).
(1)求拋物線的解析式;
(2)過點C作CD//x軸交拋物線于點D,連接AD交y軸于點E,連接AC,設△AEC的面積為S1, △DEC的面積為S2,求S1:S2的值;
(3)點F坐標為(6,0),連接D,在(2)的條件下,點P從點E出發,以每秒3個單位長的速度沿E→C→D→F勻速運動;點Q從點F出發,以每秒2個單位長的速度沿F→A勻速運動,當其中一點到達終點時,另外一點也隨之停止運動.若點P、Q同時出發,設運動時間為t秒,當t為何值時,以D、P、Q為頂點的三角形是直角三角形?請直接寫出所有符合條件的t值..
解:(1)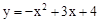
(2)
(3)當 時,以D、P、Q為頂點的三角形是直角三角形。
時,以D、P、Q為頂點的三角形是直角三角形。
解析試題分析:(1)由∵拋物線 的對稱軸是直線x=
的對稱軸是直線x= 和經過點A(—1,0),得
和經過點A(—1,0),得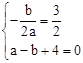 ,解之即可得拋物線的解析式。
,解之即可得拋物線的解析式。
∵拋物線 的對稱軸是直線x=
的對稱軸是直線x= ,∴
,∴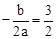 ①。
①。
又∵拋物線 經過點A(—1,0),∴
經過點A(—1,0),∴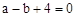 ②。
②。
聯立①②,解得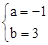 。
。
∴拋物線的解析式為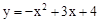 。
。
(2)根據相似三角形和等高三角形的性質,可得 和
和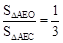 ,從而
,從而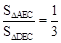 ,即S1:S2=
,即S1:S2= 。
。
在 中令x=0得
中令x=0得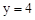 ,∴C(0,4)。
,∴C(0,4)。
∵拋物線 的對稱軸是直線x=
的對稱軸是直線x= ,CD//x軸交拋物線于點D,∴D(3,4)。
,CD//x軸交拋物線于點D,∴D(3,4)。
又OA=1,CD=3,
∵CD//x軸,∴△AEO∽△DEC。∴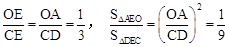 ③。
③。
又∵△AEO和△AEC是兩等高三角形,∴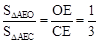 ④。
④。
③÷④,得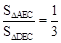 ,即S1:S2=
,即S1:S2= 。
。
(3)分四種情況討論:
①當點P在EC上運動,∠PDQ=900時,如圖1,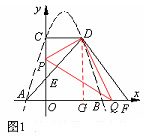
過點D作DG⊥AB于G,則CD=3,PC= 3—3t,GD=4,QG=3—2t,
由△PCD∽△QGD得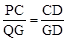 ,即
,即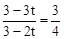 ,解得
,解得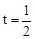 。
。
②當點P在CD上運動,∠PDQ=900時,如圖2,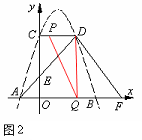
OQ=6—2t,CD=3,此時,OQDC是矩形。由OQ=CD,即6—2t=3解得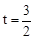 。
。
③當點P在CD上運動,∠QPD=900時,如圖3,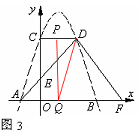
OQ=6—2t,CP=3t—3,此時,OQPC是矩形。由OQ=CP,6—2t=3t—3解得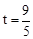 。
。
④當點P在DF上運動,∠QPD=900時,如圖4,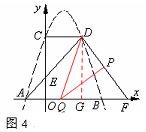
由D(3,4),F(6,0),根據勾股定理可得DF=5。
過點D作DG⊥AB于G,則DF=5,GF=3, PF= 11—3t, QF=2t,
由△FPQ∽△FGD得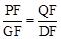 ,即
,即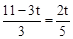 ,解得
,解得 。
。
綜上所述,當 時,以D、P、Q為頂點的三角形是直角三角形。
時,以D、P、Q為頂點的三角形是直角三角形。


科目:初中數學 來源: 題型:解答題
(本小題滿分12分)如圖,四邊形OABC為直角梯形,A(4,0),B(3,4),C(0,4).點M從O出發以每秒2個單位長度的速度向A運動;點N從B同時出發,以每秒1個單位長度的速度向C運動.其中一個動點到達終點時,另一個動點也隨之停止運動.過點N作NP垂直x軸于點P,連接AC交NP于Q,連接MQ.
(1)點 (填M或N)能到達終點;
(2)求△AQM的面積S與運動時間t的函數關系式,并寫出自變量t的取值范圍,當t為何值時,S的值最大;
(3)是否存在點M,使得△AQM為直角三角形?若存在,求出點M的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 (b,c是常數,且c<0)與x軸分別交于點A,B(點A位于點B的左側),與y軸的負半軸交于點C,點A的坐標為(-1,0).
(b,c是常數,且c<0)與x軸分別交于點A,B(點A位于點B的左側),與y軸的負半軸交于點C,點A的坐標為(-1,0).
(1)b= ,點B的橫坐標為 (上述結果均用含c的代數式表示);
(2)連接BC,過點A作直線AE∥BC,與拋物線 交于點E.點D是x軸上一點,其坐標為
交于點E.點D是x軸上一點,其坐標為
(2,0),當C,D,E三點在同一直線上時,求拋物線的解析式;
(3)在(2)的條件下,點P是x軸下方的拋物線上的一動點,連接PB,PC,設所得△PBC的面積為S.
①求S的取值范圍;
②若△PBC的面積S為整數,則這樣的△PBC共有 個.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線拋物線 (n為正整數,且0<a1<a2<…<an)與x軸的交點為An-1(bn-1,0)和An(bn,0),當n=1時,第1條拋物線
(n為正整數,且0<a1<a2<…<an)與x軸的交點為An-1(bn-1,0)和An(bn,0),當n=1時,第1條拋物線 與x軸的交點為A0(0,0)和A1(b1,0),其他依此類推.
與x軸的交點為A0(0,0)和A1(b1,0),其他依此類推.
(1)求a1,b1的值及拋物線y2的解析式;
(2)拋物線y3的頂點坐標為( , );
依此類推第n條拋物線yn的頂點坐標為( , );
所有拋物線的頂點坐標滿足的函數關系是 ;
(3)探究下列結論:
①若用An-1An表示第n條拋物線被x軸截得得線段長,直接寫出A0A1的值,并求出An-1An;
②是否存在經過點A(2,0)的直線和所有拋物線都相交,且被每一條拋物線截得得線段的長度都相等?若存在,直接寫出直線的表達式;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在直角坐標系xOy中,二次函數y=x2+(2k﹣1)x+k+1的圖象與x軸相交于O、A兩點.
(1)求這個二次函數的解析式;
(2)在這條拋物線的對稱軸右邊的圖象上有一點B,使△AOB的面積等于6,求點B的坐標;
(3)對于(2)中的點B,在此拋物線上是否存在點P,使∠POB=90°?若存在,求出點P的坐標,并求出△POB的面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商場要經營一種新上市的文具,進價為20元,試營銷階段發現:當銷售單價是25元時,每天的銷售量為250件,銷售單價每上漲1元,每天的銷售量就減少10件
(1)寫出商場銷售這種文具,每天所得的銷售利潤 (元)與銷售單價
(元)與銷售單價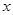 (元)之間的函數關系式;
(元)之間的函數關系式;
(2)求銷售單價為多少元時,該文具每天的銷售利潤最大;
(3)商場的營銷部結合上述情況,提出了A、B兩種營銷方案
方案A:該文具的銷售單價高于進價且不超過30元;
方案B:每天銷售量不少于10件,且每件文具的利潤至少為25元
請比較哪種方案的最大利潤更高,并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖.在平面直角坐標系中,邊長為 的正方形ABCD的頂點A、B在x軸上,連接OD、BD、△BOD的外心I在中線BF上,BF與AD交于點E.
的正方形ABCD的頂點A、B在x軸上,連接OD、BD、△BOD的外心I在中線BF上,BF與AD交于點E.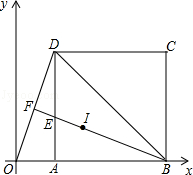
(1)求證:△OAD≌△EAB;
(2)求過點O、E、B的拋物線所表示的二次函數解析式;
(3)在(2)中的拋物線上是否存在點P,其關于直線BF的對稱點在x軸上?若有,求出點P的坐標;
(4)連接OE,若點M是直線BF上的一動點,且△BMD與△OED相似,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知二次函數 (m>0)的圖象與x軸交于A、B兩點.
(m>0)的圖象與x軸交于A、B兩點.
(1)寫出A、B兩點的坐標(坐標用m表示);
(2)若二次函數圖象的頂點P在以AB為直徑的圓上,求二次函數的解析式;
(3)設以AB為直徑的⊙M與y軸交于C、D兩點,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知點A(0,4),B(2,0).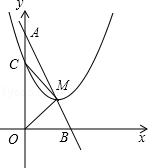
(1)求直線AB的函數解析式;
(2)已知點M是線段AB上一動點(不與點A、B重合),以M為頂點的拋物線y=(x﹣m)2+n與線段OA交于點C.
①求線段AC的長;(用含m的式子表示)
②是否存在某一時刻,使得△ACM與△AMO相似?若存在,求出此時m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com