
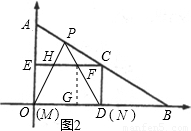
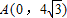 ,點B在x軸正半軸上,且∠ABO=30°,動點P在線段AB上從點A向點B以每秒
,點B在x軸正半軸上,且∠ABO=30°,動點P在線段AB上從點A向點B以每秒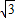 個單位的速度運動,設運動時間為t秒,在x軸上取兩點M、N作等邊△PMN.
個單位的速度運動,設運動時間為t秒,在x軸上取兩點M、N作等邊△PMN.
 )
)

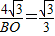
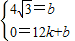
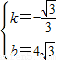
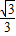 x+4
x+4
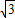
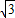 -
-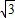 t,在Rt△MPB中,∠MPB=90°
t,在Rt△MPB中,∠MPB=90°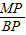
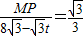
 OB=6,即8-t=6
OB=6,即8-t=6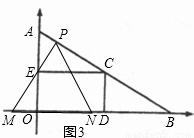
 ,
, AE=
AE= ,此時t=1
,此時t=1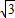
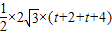
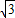 t+6
t+6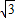
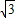 MO=4
MO=4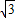 -2
-2 t
t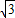 t-2
t-2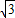
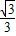 EI=2t-2
EI=2t-2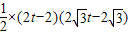
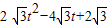
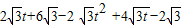


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013-2014學年浙江寧波城區五校聯考初三第一學期12月月考數學試卷(解析版) 題型:解答題
如圖1,已知拋物線y=ax2+bx(a≠0)經過A(3,0)、B(4,4)、D(2, n)三點.
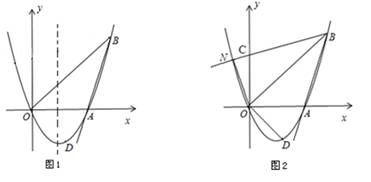
(1)求拋物線的解析式及點D坐標;
(2)點M是拋物線對稱軸上一動點,求使BM-AM的值最大時的點M的坐標;
(3)如圖2,將射線BA沿BO翻折,交y軸于點C,交拋物線于點N,求點N的坐標;
(4)在(3)的條件下,連結ON,OD,如圖2,請求出所有滿足△POD∽△NOB的點P坐標(點P、O、D分別與點N、O、B對應).
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2012年江西省宜春市中考數學模擬試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com