
【題目】綜合與實踐:
發現問題:
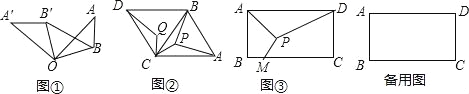
如圖①,已知:△OAB中,OB=3,將△OAB繞點O逆時針旋轉90°得△OA′B,連接BB′.
則BB′= .
問題探究:
如圖②,已知△ABC是邊長為4![]() 的等邊三角形,以BC為邊向外作等邊△BCD,P為△ABC內一點,將線段CP繞點C逆時針旋轉60°,P的對應點為Q.
的等邊三角形,以BC為邊向外作等邊△BCD,P為△ABC內一點,將線段CP繞點C逆時針旋轉60°,P的對應點為Q.
(1)求證:△DCQ≌△BCP
(2)求PA+PB+PC的最小值.
實際應用:
如圖③,某貨運場為一個矩形場地ABCD,其中AB=500米,AD=800米,頂點A、D為兩個出口,現在想在貨運廣場內建一個貨物堆放平臺P,在BC邊上(含B、C兩點)開一個貨物入口M,并修建三條專用車道PA、PD、PM.若修建每米專用車道的費用為10000元,當M,P建在何處時,修建專用車道的費用最少?最少費用為多少?
【答案】發現問題:3![]() ;問題探究:(1)證明參見解析;(2)12;實際應用:M建在BC中點(BM=400米)處,點P在過M且垂直于BC的直線上,且在M上方(500﹣
;問題探究:(1)證明參見解析;(2)12;實際應用:M建在BC中點(BM=400米)處,點P在過M且垂直于BC的直線上,且在M上方(500﹣![]() )米處,最少費用為1000000(4
)米處,最少費用為1000000(4![]() +5)萬元.
+5)萬元.
【解析】
試題分析:發現問題:根據旋轉的性質,利用勾股定理直接求得BB'的值;問題探究:(1)由等邊三角形的性質和旋轉的性質,得到△DCQ≌△BCP的條件;(2)由兩點之間線段最短得PA+PB+PC最小時的位置,用等邊三角形的性質計算;實際應用:先確定出最小值時的位置,當M,P,P1,D1在同一條直線上時,AP+PM+DP最小,最小值為D1N,再用等邊三角形的性質計算.
試題解析:發現問題:由旋轉角度可知∠BOB′=90°,OB=OB'=3,根據勾股定理得,BB′=3![]() ;問題探究:(1)∵△BDC是等邊三角形,∴CD=CB,∠DCB=60°,由旋轉得,∠PCQ=60°,PC=QC,∴∠DCQ=∠BCP,在△DCQ和△BCP中
;問題探究:(1)∵△BDC是等邊三角形,∴CD=CB,∠DCB=60°,由旋轉得,∠PCQ=60°,PC=QC,∴∠DCQ=∠BCP,在△DCQ和△BCP中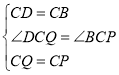 ,∴△DCQ≌△BCP;(2)如圖1,連接PQ,
,∴△DCQ≌△BCP;(2)如圖1,連接PQ,
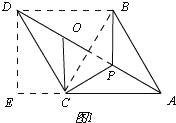 ∵PC=CQ,∠PCQ=60°∴△CPQ是等邊三角形,∴PQ=PC,由(1)有,DQ=PB,∴PA+PB+PC=AP+PQ+QD,由兩點之間線段最短得,AP+PQ+QD≥AD,∴PA+PB+PC≥AD,∴當點A,P,Q,D在同一條直線上時,PA+PB+PC取最小值為AD的長,作DE⊥AB,∵△ABC為邊長是4
∵PC=CQ,∠PCQ=60°∴△CPQ是等邊三角形,∴PQ=PC,由(1)有,DQ=PB,∴PA+PB+PC=AP+PQ+QD,由兩點之間線段最短得,AP+PQ+QD≥AD,∴PA+PB+PC≥AD,∴當點A,P,Q,D在同一條直線上時,PA+PB+PC取最小值為AD的長,作DE⊥AB,∵△ABC為邊長是4![]() 的等邊三角形,∴CB=AC=4
的等邊三角形,∴CB=AC=4![]() ,∠BCA=60°,∴CD=CB=4
,∠BCA=60°,∴CD=CB=4![]() ,∠DCE=60°,∴DE=6,∠DAE=∠ADC=30°,∴AD=12,即:PA+PB+PC的最小值為12;實際應用:如圖2,
,∠DCE=60°,∴DE=6,∠DAE=∠ADC=30°,∴AD=12,即:PA+PB+PC的最小值為12;實際應用:如圖2,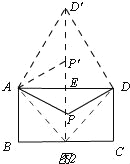 連接AM,DM,將△ADP繞點A逆時針旋轉60°,得△AP′D′,由(2)知,當M,P,P′,D′在同一條直線上時,AP+PM+DP最小,最小值為D′M,∵M在BC上,∴當D′M⊥BC時,D′M取最小值,設D′M交AD于E,∵△ADD′是等邊三角形,∴EM=AB=500,∴BM=400,PM=EM﹣PE=500﹣
連接AM,DM,將△ADP繞點A逆時針旋轉60°,得△AP′D′,由(2)知,當M,P,P′,D′在同一條直線上時,AP+PM+DP最小,最小值為D′M,∵M在BC上,∴當D′M⊥BC時,D′M取最小值,設D′M交AD于E,∵△ADD′是等邊三角形,∴EM=AB=500,∴BM=400,PM=EM﹣PE=500﹣![]() ,∴D′E=
,∴D′E=![]() AD=400
AD=400![]() ,∴D′M=400
,∴D′M=400![]() +500,∴最少費用為10000×(400
+500,∴最少費用為10000×(400![]() +500)=1000000(4
+500)=1000000(4![]() +5)萬元;∴M建在BC中點(BM=400米)處,點P在過M且垂直于BC的直線上,且在M上方(500﹣
+5)萬元;∴M建在BC中點(BM=400米)處,點P在過M且垂直于BC的直線上,且在M上方(500﹣![]() )米處,最少費用為1000000(4
)米處,最少費用為1000000(4![]() +5)萬元.
+5)萬元.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知平行四邊形ABCD中,對角線AC,BD相交于點O,過點O的直線分別交AD,BC于點E,F,則圖中的全等三角形共有( )

A. 2對 B. 4對 C. 6對 D. 8對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星期天,玲玲騎自行車到郊外游玩,她離家的距離與時間的關系如圖所示,請根據圖像回答下列問題.

(1)玲玲到達離家最遠的地方是什么時間?離家多遠?
(2)她何時開始第一次休息?休息了多長時間?
(3)她騎車速度最快是在什么時候?車速多少?
(4)玲玲全程騎車的平均速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是反比例函數 ![]() 在第二象限內圖象上一點,點B是反比例函數
在第二象限內圖象上一點,點B是反比例函數 ![]() 在第一象限內圖象上一點,直線AB與y軸交于點C,且AC=BC,連接OA、OB,則△AOB的面積是 .
在第一象限內圖象上一點,直線AB與y軸交于點C,且AC=BC,連接OA、OB,則△AOB的面積是 . 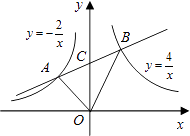
查看答案和解析>>
科目:初中數學 來源: 題型:
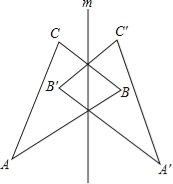
【題目】如圖,△ABC和△A′B′C′關于直線m對稱.
(1)結合圖形指出對稱點.
(2)連接A、A′,直線m與線段AA′有什么關系?
(3)延長線段AC與A′C′,它們的交點與直線m有怎樣的關系?其它對應線段(或其延長線)的交點呢?你發現了什么規律,請敘述出來與同伴交流.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com