
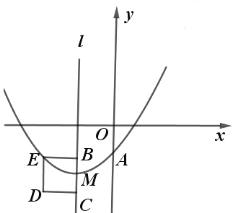
【題目】如圖,拋物線![]()
![]() 過點
過點![]() ,頂點
,頂點![]() 在第三象限,
在第三象限,![]() ,
,![]() 是拋物線的對稱軸
是拋物線的對稱軸![]() 上的兩點,且
上的兩點,且![]() ,在直線
,在直線![]() 左側以
左側以![]() 為邊作正方形
為邊作正方形![]() ,點
,點![]() 恰好在拋物線上.
恰好在拋物線上.
(1)用含![]() 的式子表示
的式子表示![]() ;
;
(2)求證:點![]() 和點
和點![]() 關于直線
關于直線![]() 對稱;
對稱;
(3)判斷直線![]() 和直線
和直線![]() (
(![]() 是常數,且
是常數,且![]() )的交點是否在拋物線上,并說明理由.
)的交點是否在拋物線上,并說明理由.
 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源: 題型:
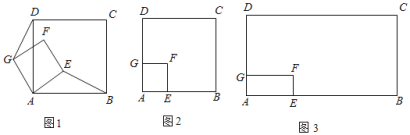
【題目】(1)問題探究:如圖1所示,有公共頂點A的兩個正方形ABCD和正方形AEFG.AE<AB,連接BE與DG,請判斷線段BE與線段DG之間有怎樣的數量關系和位置關系.并請說明理由.
(2)理解應用:如圖2所示,有公共頂點A的兩個正方形ABCD和正方形AEFG,AE<AB,AB=10,將正方形AEFG繞點A在平面內任意旋轉,當∠ABE=15°,且點D、E、G三點在同一條直線上時,請直接寫出AE的長 ;
(3)拓展應用:如圖3所示,有公共頂點A的兩個矩形ABCD和矩形AEFG,AD=4![]() ,AB=4
,AB=4![]() ,AG=4,AE=4
,AG=4,AE=4![]() ,將矩形AEFG繞點A在平面內任意旋轉,連接BD,DE,點M,N分別是BD,DE的中點,連接MN,當點D、E、G三點在同一條直線上時,請直接寫出MN的長
,將矩形AEFG繞點A在平面內任意旋轉,連接BD,DE,點M,N分別是BD,DE的中點,連接MN,當點D、E、G三點在同一條直線上時,請直接寫出MN的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸的交點
軸的交點![]() 在點
在點![]() 與點
與點![]() 之間(不包括這兩點),對稱軸為直線
之間(不包括這兩點),對稱軸為直線![]() .有下列結論:
.有下列結論:
①![]() ;②
;②![]() ;③
;③![]() ;④若點
;④若點![]() ,
,![]() 在拋物線上,則
在拋物線上,則![]() .其中正確結論的個數是()
.其中正確結論的個數是()
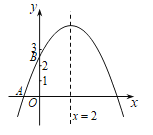
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
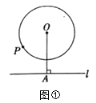
【題目】問題探究
(1)如圖①,已知![]() 與直線
與直線![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,
,![]() ,
,![]() 的半徑為
的半徑為![]() ,則圓上一點
,則圓上一點![]() 到
到![]() 的距離的最小值是______;
的距離的最小值是______;
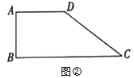
(2)如圖②,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作一條直線交邊
作一條直線交邊![]() 或
或![]() 于
于![]() ,若
,若![]() 平分四邊形
平分四邊形![]() 的面積,求
的面積,求![]() 的長;
的長;
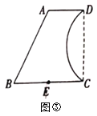
問題解決
(3)如圖③所示,是由線段![]() 、
、![]() 、
、![]() 與弧
與弧![]() 圍成的花園的平面示意圖,
圍成的花園的平面示意圖,![]() ,
,![]() ,
,![]() //
//![]() ,CD⊥BC,點
,CD⊥BC,點![]() 為
為![]() 的中點,
的中點,![]() 所對的圓心角為
所對的圓心角為![]() .管理人員想在
.管理人員想在![]() 上確定一點
上確定一點![]() ,在四邊形
,在四邊形![]() 區域種植花卉,其余區域種植草坪,并過
區域種植花卉,其余區域種植草坪,并過![]() 點修建一條小路
點修建一條小路![]() ,把四邊形
,把四邊形![]() 分成面積相等且盡可能小的兩部分,分別種植不同的花卉.問是否存在滿足上述條件的小路
分成面積相等且盡可能小的兩部分,分別種植不同的花卉.問是否存在滿足上述條件的小路![]() ?若存在,請求出
?若存在,請求出![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象與
的圖象與![]() 軸的交點坐標為
軸的交點坐標為![]() 和
和![]() .
.
(1)求![]() 和
和![]() (用
(用![]() 的代數式表示);
的代數式表示);
(2)若在自變量![]() 的值滿足
的值滿足![]() 的情況下,與其對應的函數值
的情況下,與其對應的函數值![]() 的最大值為1,求
的最大值為1,求![]() 的值;
的值;
(3)已知點![]() 和點
和點![]() .若二次函數
.若二次函數![]() 的圖象與線段
的圖象與線段![]() 有兩個不同的交點,直接寫出
有兩個不同的交點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乒乓球是我國的國球,比賽采用單局![]() 分制,分團體、單打、雙打等。在某站公開賽中,某直播平臺同時直播
分制,分團體、單打、雙打等。在某站公開賽中,某直播平臺同時直播![]() 場男單四分之一決賽,四場比賽的球桌號分別為“
場男單四分之一決賽,四場比賽的球桌號分別為“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”(假設
”(假設![]() 場比賽同時開始),小寧和父親準備一同觀看其中的一場比賽,但兩人的意見不統一,于是采用抽簽的方式決定,抽簽規則如下:將正面分別寫有數字“
場比賽同時開始),小寧和父親準備一同觀看其中的一場比賽,但兩人的意見不統一,于是采用抽簽的方式決定,抽簽規則如下:將正面分別寫有數字“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”的四張卡片(除數字不同外,其余均相同)分別對應球桌號“
”的四張卡片(除數字不同外,其余均相同)分別對應球桌號“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”,卡片洗勻后背面朝上放在桌子上,父親先從中隨機抽取一張,小寧再從剩下的
”,卡片洗勻后背面朝上放在桌子上,父親先從中隨機抽取一張,小寧再從剩下的![]() 張卡片中隨機抽取一張,比較兩人所抽卡片上的數字,觀看較大的數字對應球桌的比賽。
張卡片中隨機抽取一張,比較兩人所抽卡片上的數字,觀看較大的數字對應球桌的比賽。
(1)下列事件中屬于必然事件的是 .
A.抽到的是小寧最終想要看的一場比賽的球桌號
B.抽到的是父親最終想要看的一場比賽的球桌號
C.小寧和父親抽到同一個球桌號
D.小寧和父親抽到的球桌號不一樣
(2)用列表法或樹狀圖法求小寧和父親最終觀看“T”球桌比賽的概率。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() :
:![]() 和二次函數
和二次函數![]() :
:![]()
![]() 圖象的頂點分別為
圖象的頂點分別為![]() 、
、![]() ,與
,與![]() 軸分別相交于
軸分別相交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊)和
的左邊)和![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊),
的左邊),
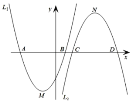
(1)函數![]() 的頂點坐標為______;當二次函數
的頂點坐標為______;當二次函數![]() ,
,![]() 的
的![]() 值同時隨著
值同時隨著![]() 的增大而增大時,則
的增大而增大時,則![]() 的取值范圍是_______;
的取值范圍是_______;
(2)判斷四邊形![]() 的形狀(直接寫出,不必證明);
的形狀(直接寫出,不必證明);
(3)拋物線![]() ,
,![]() 均會分別經過某些定點;
均會分別經過某些定點;
①求所有定點的坐標;
②若拋物線![]() 位置固定不變,通過平移拋物線
位置固定不變,通過平移拋物線![]() 的位置使這些定點組成的圖形為菱形,則拋物線
的位置使這些定點組成的圖形為菱形,則拋物線![]() 應平移的距離是多少?
應平移的距離是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
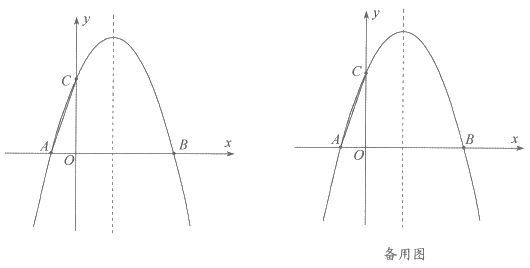
【題目】如圖,已知拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 兩點,點
兩點,點![]() 坐標為
坐標為![]() ,拋物線的對稱軸是直線
,拋物線的對稱軸是直線![]()
(1)求拋物線的解析式;
(2)點![]() 是
是![]() 軸右側拋物線圖像上的一動點,設點
軸右側拋物線圖像上的一動點,設點![]() 的橫坐標為
的橫坐標為![]() .
.
①是否存在這樣的點![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
②若該動點![]() 在第一象限內,連接
在第一象限內,連接![]() ,當
,當![]() 時,求
時,求![]() 的值
的值
查看答案和解析>>
科目:初中數學 來源: 題型:
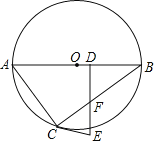
【題目】如圖,已知AB是⊙O的直徑,C是⊙O上的一點,D是AB上的一點,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求證:EC是⊙O的切線;
(2)若BD=4,BC=8,圓的半徑OB=5,求切線EC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com