
【題目】如圖![]() ,在平面直角坐標系中,直線
,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() ,點
,點![]() ,點
,點![]() 在
在![]() 軸上.
軸上.
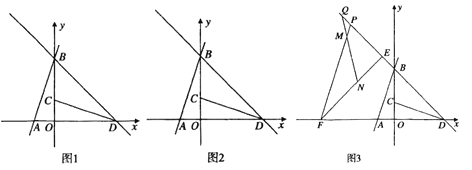
(1)求直線![]() 的解析式;
的解析式;
(2)點![]() 是直線
是直線![]() 在第二象限內一點,直線
在第二象限內一點,直線![]() 交
交![]() 軸于點
軸于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的解析式;
的解析式;
(3)如圖![]() ,在(2)的條件下,
,在(2)的條件下,![]() 、
、![]() 是
是![]() 延長線上的兩點(點
延長線上的兩點(點![]() 在點
在點![]() 的右側),
的右側),![]() ,連接
,連接![]() ,
,![]() 是
是![]() 上一點,直線
上一點,直線![]() 交
交![]() 于點
于點![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)現根據題意確定B,D的坐標,然后用待定系數法即可求解;(2)過點![]() 作
作![]() 于點
于點![]() .由(1)可知
.由(1)可知![]() .可得△EDF是等腰直角三角形.即
.可得△EDF是等腰直角三角形.即![]() .然后根據題意確定E的坐標和EH的表達式,然后看圖寫出四邊形ABEF的面積表達式;(3)過點
.然后根據題意確定E的坐標和EH的表達式,然后看圖寫出四邊形ABEF的面積表達式;(3)過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,在
,在![]() 延長線上截取
延長線上截取![]() ,連接
,連接![]() ,然后說明四邊形
,然后說明四邊形![]() 是平行四邊形,四邊形
是平行四邊形,四邊形![]() 是正方形以及
是正方形以及![]() ,最后運用勾股定理完成解答.
,最后運用勾股定理完成解答.
解:(1)∵![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() .設直線
.設直線![]() 的解析式為
的解析式為![]() ,把
,把![]() ,
,![]() 代入,解得
代入,解得![]() ,
,![]() .∴
.∴![]() .
.

(2)過點![]() 作
作![]() 于點
于點![]() .由(1)可知
.由(1)可知![]() .
.
∴△EDF是等腰直角三角形.
∴![]() .
.
由題意知![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.

(3)如圖,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,在
,在![]() 延長線上截取
延長線上截取![]() ,連接
,連接![]() .∵
.∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴四邊形
,∴四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,![]() .∴
.∴![]() .∴
.∴![]() .易得
.易得![]() ,∴
,∴![]() .∴易證四邊形
.∴易證四邊形![]() 是正方形.∴
是正方形.∴![]() .∴
.∴![]() .∴
.∴![]() ,
,![]() .∵
.∵![]() ,∴
,∴![]() .∴
.∴![]() .設
.設![]() ,則
,則![]() .∵
.∵![]() ,∴
,∴![]() .
.
∴在![]() 中,由勾股定理得
中,由勾股定理得![]() ,解得
,解得![]() ,
,![]() (舍去).∴
(舍去).∴![]() .∴
.∴![]() .∴
.∴![]() .
.


科目:初中數學 來源: 題型:
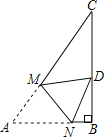
【題目】如圖,已知Rt△ABC中,∠B=90°,∠A=60°,AC=3,點M、N分別在線段AC、AB上,將△ANM沿直線M折疊,使點A的對應點D恰好落在線段BC上,當△DCM為直角三角形時,折痕MN的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市銷售一種文具,進價為5元/件.售價為6元/件時,當天的銷售量為100件.在銷售過程中發現:售價每上漲0.5元,當天的銷售量就減少5件.設當天銷售單價統一為![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍數上漲),當天銷售利潤為
是按0.5元的倍數上漲),當天銷售利潤為![]() 元.
元.
(1)求![]() 與
與![]() 的函數關系式(不要求寫出自變量的取值范圍);
的函數關系式(不要求寫出自變量的取值范圍);
(2)要使當天銷售利潤不低于240元,求當天銷售單價所在的范圍;
(3)若每件文具的利潤不超過![]() ,要想當天獲得利潤最大,每件文具售價為多少元?并求出最大利潤.
,要想當天獲得利潤最大,每件文具售價為多少元?并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() 的頂點
的頂點![]() 、
、![]() 在
在![]() 上,頂點
上,頂點![]() 、
、![]() 在
在![]() 內,將正方形
內,將正方形![]() 繞點
繞點![]() 逆時針旋轉,使點
逆時針旋轉,使點![]() 落在
落在![]() 上.若正方形
上.若正方形![]() 的邊長和
的邊長和![]() 的半徑均為
的半徑均為![]() ,則點
,則點![]() 運動的路徑長為( )
運動的路徑長為( )
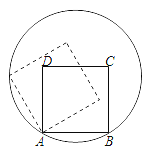
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
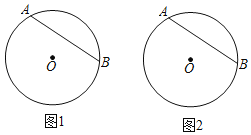
【題目】在⊙O中,![]() 的度數為120°,點P為弦AB上的一點,連結OP并延長交⊙O于點C,連結OB,AC.
的度數為120°,點P為弦AB上的一點,連結OP并延長交⊙O于點C,連結OB,AC.
(1)若P為AB中點,且PC=1,求圓的半徑.
(2)若BP:BA=1:3,請求出tan∠OPA.
查看答案和解析>>
科目:初中數學 來源: 題型:
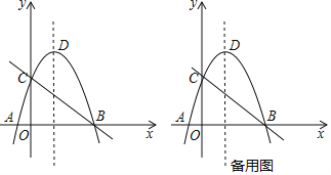
【題目】如圖,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 兩點,拋物線
兩點,拋物線![]() 經過點
經過點![]() ,與
,與![]() 軸另一交點為
軸另一交點為![]() ,頂點為
,頂點為![]() .
.
(1)求拋物線的解析式;
(2)在![]() 軸上找一點
軸上找一點![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在拋物線的對稱軸上是否存在一點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
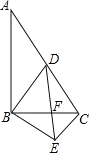
【題目】如圖,在![]() 中,
中,![]() 為斜邊
為斜邊![]() 的中點,連接
的中點,連接![]() ,點
,點![]() 是
是![]() 邊上的動點(不與點
邊上的動點(不與點![]() 重合),過點
重合),過點![]() 作
作![]() 交
交![]() 延長線交于點
延長線交于點![]() ,連接
,連接![]() ,下列結論:
,下列結論:
①若![]() ,則
,則![]() ;
;
②若![]() ,則
,則![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,則
,則![]() .
.
其中正確的是_____.(填寫所有正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寒梅中學為了豐富學生的課余生活,計劃購買圍棋和中國象棋供棋類興趣小組活動使用,若購買3副圍棋和5副中國象棋需用98元;若購買8副圍棋和3副中國象棋需用158元;(1)求每副圍棋和每副中國象棋各多少元;(2)寒梅中學決定購買圍棋和中國象棋共40副,總費用不超過550元,那么寒梅中學最多可以購買多少副圍棋?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com