
【題目】2020年,新型冠狀病毒席卷全球,疫情當前,全國上下砥礪同行.某中學校指導中心為引導未成年人以健康心理、陽光心態抗擊疫情,積極開展了心理援助工作,并推出“你是我的奧特曼”有獎征稿活動.活動結束后,該指導中心對參賽學生的獲獎情況進行統計,并繪制了如下兩幅不完整的統計圖.
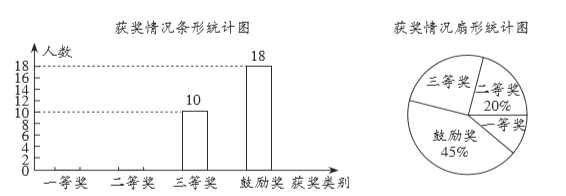
結合圖中的相關數據,解答下列問題:
(1)參加此次有獎征稿活動的學生有 人,在扇形統計圖中,“三等獎”所對應扇形的圓心角度數為 ;
(2)將條形統計圖補充完整;
(3)若獲得“一等獎”的學生中有![]() 來自七年級,
來自七年級,![]() 來自九年級,其余來自八年級,學校決定從獲得“一等獎”的學生中任選2名作為代表在線上分享心靈戰“疫”小錦囊,請用列表或畫樹狀圖的方法求所選2名學生中恰好是1名七年級和1名九年級學生的概率.
來自九年級,其余來自八年級,學校決定從獲得“一等獎”的學生中任選2名作為代表在線上分享心靈戰“疫”小錦囊,請用列表或畫樹狀圖的方法求所選2名學生中恰好是1名七年級和1名九年級學生的概率.
【答案】(1)40 ,90°;(2)見解析;(3)![]()
【解析】
(1)用獲得鼓勵獎的人數除以其所占比例可得參加活動的學生總人數,用10除以總人數再乘以360°即為“三等獎”所對應扇形的圓心角;
(2)用總人數×20%即得獲得“二等獎”的學生人數,用總人數減去其它三個組的人數即為獲得“一等獎”的學生人數,進而可補全條形統計圖;
(3)先根據題意求出獲得“一等獎”的學生中,七年級、八年級和九年級的學生人數,然后畫出樹狀圖求出所有可能的結果數,找出恰好是1名七年級和1名九年級學生的結果數,再根據概率公式計算即可.
解:(1)18÷45%=40(人),![]() ×360°=90°;
×360°=90°;
故答案為:40,90°;
(2)獲得“二等獎”的學生人數為40×20%=8(人),則獲得“一等獎”的學生人數為40-8-10-18=4(人).
補全條形統計圖如圖所示:
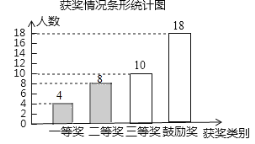
(3)由題意,知獲得“一等獎”的學生中,七年級有1人,八年級有1人,九年級有2人,分別用A,B,C1,C2表示七年級、八年級和九年級的學生.畫樹狀圖如下:

由圖可知,所有等可能的結果共12種,其中所選的2名學生中1名是七年級1名是九年級的結果有4種,
所以P(所選2名學生中恰好是1名七年級和1名九年級學生)=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
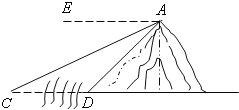
【題目】如圖,河旁有一座小山,從山頂A處測得河對岸點C的俯角為30°,測得岸邊點D的俯角為45°,現從山頂A到河對岸點C拉一條筆直的纜繩AC,如果AC是120米,求河寬CD的長?
查看答案和解析>>
科目:初中數學 來源: 題型:
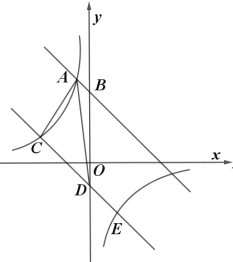
【題目】如圖在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與反比例函數
,與反比例函數![]() 在第二象限內的圖象相交于點
在第二象限內的圖象相交于點![]() .
.
![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 將直線
將直線![]() 向下平移
向下平移![]() 個單位后與反比例函數的圖象交于點
個單位后與反比例函數的圖象交于點![]() 和點
和點![]() 與
與![]() 軸交于點
軸交于點![]() 求
求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,經過
,經過![]() 、
、![]() 兩點的拋物線
兩點的拋物線![]() 與
與![]() 軸的另一交點
軸的另一交點![]() .
.
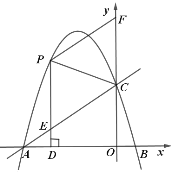
(1)求該拋物線的函數表達式;
(2)![]() 是該拋物線上的動點,過點
是該拋物線上的動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
①求出四邊形![]() 的周長
的周長![]() 與
與![]() 的函數表達式,并求
的函數表達式,并求![]() 的最大值;
的最大值;
②當![]() 為何值時,四邊形
為何值時,四邊形![]() 是菱形;
是菱形;
③是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出滿足條件的點
相似?若存在,請求出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
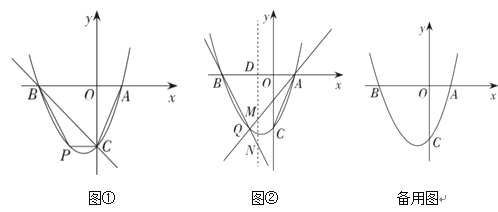
【題目】如圖①,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() ,
,![]() ,拋物線
,拋物線![]() 經過
經過![]() ,
,![]() 兩點,且與
兩點,且與![]() 軸的另一交點為
軸的另一交點為![]() .
.
(1)求拋物線的函數解析式;
(2)如圖①,點![]() 在第三象限內的拋物線上.
在第三象限內的拋物線上.
①連接![]() ,
,![]() ,
,![]() ,當四邊形
,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
②![]() 為
為![]() 軸上一點,當
軸上一點,當![]() 取得最小值時,求點
取得最小值時,求點![]() 的坐標;
的坐標;
(3)如圖②,![]() 為
為![]() 軸下方拋物線上任意一點,
軸下方拋物線上任意一點,![]() 是拋物線的對稱軸與
是拋物線的對稱軸與![]() 軸的交點,直線
軸的交點,直線![]() ,
,![]() 分別交拋物線的對稱軸于點
分別交拋物線的對稱軸于點![]() ,
,![]() .問:
.問:![]() 是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游樂園有一個直徑為16米的圓形噴水池,噴水池的周邊有一圈噴水頭,噴出的水柱為拋物線,在距水池中心3米處達到最高,高度為5米,且各方向噴出的水柱恰好在噴水池中心的裝飾物處匯合.如圖所示,以水平方向為x軸,噴水池中心為原點建立直角坐標系.
(1)求水柱所在拋物線(第一象限部分)的函數表達式;
(2)王師傅在噴水池內維修設備期間,噴水管意外噴水,為了不被淋濕,身高1.8米的王師傅站立時必須在離水池中心多少米以內?
(3)經檢修評估,游樂園決定對噴水設施做如下設計改進:在噴出水柱的形狀不變的前提下,把水池的直徑擴大到32米,各方向噴出的水柱仍在噴水池中心保留的原裝飾物(高度不變)處匯合,請探究擴建改造后噴水池水柱的最大高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() 為常數)的頂點為
為常數)的頂點為![]() .
.
(1)求點![]() 的坐標;(用含
的坐標;(用含![]() 的式子表示)
的式子表示)
(2)在同一平面直角坐標系中,存在函數圖象![]() ,點
,點![]() 在圖象
在圖象![]() 上,點
上,點![]() 在拋物線
在拋物線![]() 上,對于任意的實數
上,對于任意的實數![]() ,都有點
,都有點![]() ,
,![]() 關于點
關于點![]() 對稱.
對稱.
①當![]() 時,求圖象
時,求圖象![]() 對應函數的解析式;
對應函數的解析式;
②當![]() 時,都有
時,都有![]() 成立,結合圖象,求
成立,結合圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,平面直角坐標系xOy中,矩形ABCD的邊AB=4,BC=6.在不改變矩形ABCD的形狀和大小的情況下,當矩形的頂點A在x軸的正半軸上左右移動時,另一個頂點D始終在y軸的正半軸上隨之上下移動.
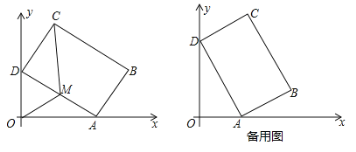
(1)當∠OAD=30°時,求點C的坐標;
(2)設AD的中點為M,連接OM、MC,若四邊形OMCD的面積為![]() 時,求OA的長;
時,求OA的長;
(3)在點A移動過程中是否存在某一位置,使點C到點O的距離有最大值?若存在,求此時的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com