【題目】下面是小東設計的“過直線外一點作這條直線的平行線”的尺規作圖過程．
已知：直線l及直線l外一點P．
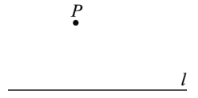
求作：直線
，使得
．
作法：如圖，
①任意取一點K，使點K和點P在直線l的兩旁；
②以P為圓心，
長為半徑畫弧，交l于點
，連接
；
③分別以點
為圓心，以
長為半徑畫弧，兩弧相交于點Q（點Q和點A在直線
的兩旁）；
④作直線．
所以直線就是所求作的直線．
根據小東設計的尺規作圖過程，
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：連接
，
______，
______，
四邊形
是平行四邊形（__________）（填推理依據）．
．
科目：初中數學 來源： 題型：
【題目】某工廠接受了20天內生產1200臺AB型電子產品的總任務．已知每臺AB型產品由4個A型裝置和3個B型裝置配套組成．工廠現有80名工人，每個工人每天能加工6個A型裝置或3個B型裝置．工廠將所有工人分成兩組同時開始加工，每組分別加工一種裝置，并要求每天加工的A、B型裝置數量正好全部配套組成AB型產品．為了在規定期限內完成總任務，工廠決定補充一些新工人，這些新工人只能獨立進行A型裝置的加工，且每人每天只能加工4個A型裝置．
（1）設原來每天安排x名工人生產A型裝置，后來補充m名新工人，求x的值（用含m的代數式表示）
（2）請問至少需要補充多少名新工人才能在規定期內完成總任務？
查看答案和解析>>
科目：初中數學 來源： 題型：
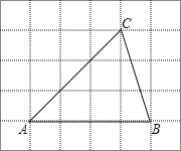
【題目】如圖，將
放在每個小正方形的邊長為1的網格中，點A、B、C均落在格點上．
Ⅰ
的面積等于______；
Ⅱ
若四邊形DEFG是中所能包含的面積最大的正方形，請你在如圖所示的網格中，用直尺和三角尺畫出該正方形，并簡要說明畫圖方法不要求證明________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為緩解某學校大班額現狀，某市決定通過新建學校來解決該問題．經測算，建設6個小學，5個中學，需費用13800萬元，建設10個小學，7個中學，需花費20600萬元．
（1）求建設一個小學，一個中學各需多少費用．
（2）該市共計劃建設中小學80所，其中小學的建設數量不超過中學建設數量的1.5倍．設建設小學的數量為x個，建設中小學校的總費用為y萬元．
①求y關于x的函數關系式；
②如何安排中小學的建設數量，才能使建設總費用最低？
（3）受國家開放二胎政策及外來務工子女就讀的影響，預計在小學就讀人數會有明顯增加，現決定在（2）中所定的方案上增加投資以擴大小學的就讀規模，若建設小學總費用不超過建設中學的總費用，則每所小學最多可增加多少費用？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為鼓勵下崗工人再就業，某地市政府規定，企業按成本價提供產品給下崗人員自主銷售，成本價與出廠價之間的差價由政府承擔．老李按照政策投資銷售本市生產的一種兒童面條．已知這種兒童面條的成本價為每袋12元，出廠價為每袋16元，每天銷售量
（袋）與銷售單價
（元）之間的關系近似滿足一次函數：
．
（1）老李在開始創業的第1天將銷售單價定為17元，那么政府這一天為他承擔的總差價為多少元？
（2）設老李獲得的利潤為
（元），當銷售單價為多少元時，每天可獲得最大利潤？
（3）物價部門規定，這種面條的銷售單價不得高于24元，如果老李想要每天獲得的利潤不低于216元，那么政府每天為他承擔的總差價最少為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于平面直角坐標系
中的點P和圖形M，給出如下定義：Q為圖形M上任意一點，如果
兩點間的距離有最大值，那么稱這個最大值為點P與圖形M間的開距離，記作
．已知直線
與x軸交于點A，與y軸交于點B，
的半徑為1．
（1）若
，
①求
的值；
②若點C在直線
上，求
的最小值；
（2）以點A為中心，將線段順時針旋轉
得到
，點E在線段
組成的圖形上，若對于任意點E，總有
，直接寫出b的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖（1），在
中，
，
，點
分別是
的中點，過點
作直線
的垂線段
垂足為
．點
是直線
上一動點，作
使
，
連接
．
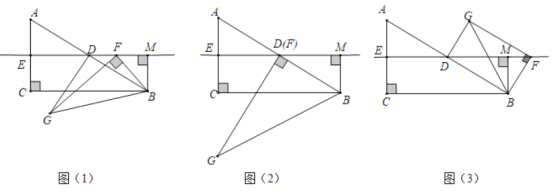
（1）觀察猜想：如圖（2），當點與點
重合時，則
的值為 ．
（2）問題探究：如圖（1），當點與點不重合時，請求出的值及兩直線
夾角銳角的度數，并說明理由
（3）問題解決：如圖（3），當點
在同一直線上時，請直接寫出
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中的三點A(1，0)，B(－1，0)，P(0，－1)，將線段AB沿y軸向上平移m(m＞0)個單位長度，得到線段CD，二次函數y＝a(x－h)2＋k的圖象經過點P，C，D．
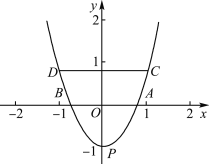
(1)當m＝1時，a＝______；當m＝2時，a＝______；
(2)猜想a與m的關系，并證明你的猜想；
(3)將線段AB沿y軸向上平移n(n＞0)個單位長度，得到線段C1D1，點C1，D1分別與點A，B對應，二次函數y＝2a(x－h)2＋k的圖象經過點P，C1，D1．
①求n與m之間的關系；
②當△COD1是直角三角形時，直接寫出a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
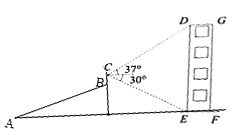
【題目】某同學利用數學知識測量建筑物DEFG的高度．他從點
出發沿著坡度為
的斜坡AB步行26米到達點B處，用測角儀測得建筑物頂端
的仰角為37°，建筑物底端
的俯角為30°，若AF為水平的地面，側角儀豎直放置，其高度BC=1.6米，則此建筑物的高度DE約為(精確到
米，參考數據：
，
)（ ）
A.
米B.
米C.
米D.
米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
