
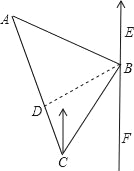
【題目】如圖,一貨輪在C處測得燈塔A在貨輪的北偏西30°的方向上,隨后貨輪以60海里/時的速度按北偏東30°的方向航行,半小時后到達B處,此時又測得燈塔A在貨輪的北偏西75°的方向上(如圖),求此時貨輪距燈塔A的距離AB.

【答案】15![]()
【解析】
此題可先由速度和時間求出BC的距離,再由各方向角得出∠A的角度,過B作BD⊥AC于D,求出∠DBC=30°,求出DC,由勾股定理求出BD,求出AD、BD的長,由勾股定理求出AB即可.
由示意圖可知:∠ACB=60°,
由平行線的性質可知∠ABC=180°﹣30°﹣75°=75°,
∴∠A=180°﹣∠C﹣∠B=45°,BC=60×![]() =30(海里),
=30(海里),
過B作BD⊥AC于D,
則∠BDC=90°,∠DBC=30°,
∴DC=![]() BC=15海里,
BC=15海里,
由勾股定理得:BD=15![]() 海里,
海里,
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=15![]() 海里,
海里,
由勾股定理得:AB=![]() (海里),
(海里),
答:此時貨輪距燈塔A的距離AB為![]() 海里.
海里.


科目:初中數學 來源: 題型:
【題目】某商品的進價為每件50元.當售價為每件70元時,每星期可賣出300件,現需降價處理,且經市場調查:每降價1元,每星期可多賣出20件.在確保盈利的前提下,解答下列問題:
(1)若設每件降價x元、每星期售出商品的利潤為y元,請寫出y與x的函數關系式,并求出自變量x的取值范圍;
(2)當降價多少元時,每星期的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
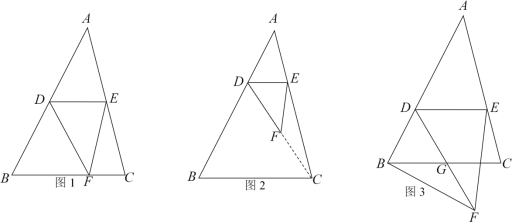
【題目】已知△ABC中,∠B= 60°,點D是AB邊上的動點,過點D作DE∥BC交AC于點E,將△ABE沿DE折疊,點A對應點為F點.
(1)如圖1,當點F恰好落在BC邊上,求證:△BDF是等邊三角形;
(2)如圖2,當點F恰好落在△ABC內,且DF的延長線恰好經過點C,CF=EF,求∠A的大小;
(3)如圖3,當點F恰好落在△ABC外,DF交BC于點G,連接BF,若BF⊥AB,AB=9,求BG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,且點
兩點,且點![]() 的橫坐標和點
的橫坐標和點![]() 的縱坐標都是
的縱坐標都是![]() ,求:
,求:

![]() 一次函數的解析式;(2)
一次函數的解析式;(2)![]() 的面積.
的面積.
![]() 根據圖象回答:當
根據圖象回答:當![]() 為何值時,一次函數的函數值大于反比例函數的函數值.
為何值時,一次函數的函數值大于反比例函數的函數值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com