
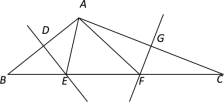
【題目】如圖,在△ABC中,∠BAC=120°,若DE,FG分別垂直平分AB,AC,△AEF的周長(zhǎng)為10cm,求BC的長(zhǎng)及∠EAF的度數(shù).
【答案】10;60°
【解析】
①根據(jù)線(xiàn)段垂直平分線(xiàn)的性質(zhì)求出△EAF的周長(zhǎng)證明△EAF與BC的關(guān)系從而求出BC的長(zhǎng)度;②根據(jù)三角形內(nèi)角和定理求出∠B+∠C=60°,再根據(jù)線(xiàn)段垂直平分線(xiàn)的性質(zhì)求出∠BAE+∠CAF=∠B+∠C,然后求出∠EAF.
解:①∵DE,FG分別垂直平分邊AB,AC,
∴EA=EB,FA=FC,
∴△EAF的周長(zhǎng)=EA+FA+EF=BE+EF+FC=BC
∴BC=10;
②∵∠BAC=120°,
∴∠B+∠C=180°-120°=60°,
∵DE、FG分別垂直平分AB和AC,
∴∠BAE=∠B,∠CAF=∠C,
∴∠BAE+∠CAF=60°,
∴∠EAF=120°-60°=60°.
故答案為:10;60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,![]() ,
,![]() ,
,![]() ,給出下列結(jié)論:①
,給出下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結(jié)論是( )
.其中正確的結(jié)論是( )
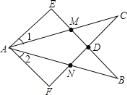
A. ①② B. ②③ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
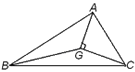
【題目】如圖:在△ABC中,G是它的重心,AG⊥CD,如果![]() ,則△AGC的面積的最大值是( )
,則△AGC的面積的最大值是( )
A. ![]() B. 8 C.
B. 8 C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,工人師傅常用“卡鉗”這種工具測(cè)定工件內(nèi)槽的寬.卡鉗由兩根鋼條AA′、BB′組成,O為AA′、BB′的中點(diǎn).只要量出A′B′的長(zhǎng)度,由三角形全等就可以知道工件內(nèi)槽AB的長(zhǎng)度.則判定△OAB≌△OA′B′的依據(jù)是( )

A. SASB. ASAC. SSSD. AAS
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
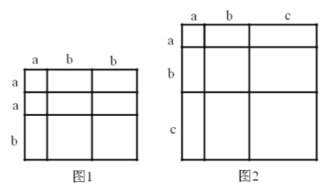
【題目】閱讀下列文字,對(duì)于一個(gè)圖形,通過(guò)不同的方法計(jì)算圖形的面積,可以得到一個(gè)數(shù)學(xué)等式,例如:由圖1可以得到![]() ,請(qǐng)解答下列問(wèn)題:
,請(qǐng)解答下列問(wèn)題:
(1)寫(xiě)出圖2中所表示的數(shù)學(xué)等式 ;
(2)利用(1)中所得到的結(jié)論,解決問(wèn)題:已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列語(yǔ)句:①-1是1的平方根。②帶根號(hào)的數(shù)都是無(wú)理數(shù)。③-1的立方根是-1。④![]() 的立方根是2。⑤(-2)2的算術(shù)平方根是2。⑥-125的立方根是±5。⑦有理數(shù)和數(shù)軸上的點(diǎn)一一對(duì)應(yīng)。其中正確的有( )
的立方根是2。⑤(-2)2的算術(shù)平方根是2。⑥-125的立方根是±5。⑦有理數(shù)和數(shù)軸上的點(diǎn)一一對(duì)應(yīng)。其中正確的有( )
A. 2個(gè)B. 3個(gè)C. 4個(gè)D. 5個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
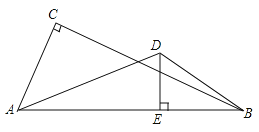
【題目】如圖,學(xué)校位于高速路AB的一側(cè)(AB成一條直線(xiàn)),點(diǎn)A,B為高速路上距學(xué)校直線(xiàn)距離最近的2個(gè)隧道出入口,點(diǎn)C、D為學(xué)校的兩棟教學(xué)樓,經(jīng)測(cè)量∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,點(diǎn)D到高速路的最短直線(xiàn)距離DE=400m.
(1)求教學(xué)樓C到隧道口B的直線(xiàn)距離;
(2)比較AC2+BC2與AD2+BD2誰(shuí)大誰(shuí)小,試用計(jì)算說(shuō)明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
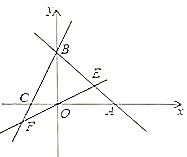
【題目】直線(xiàn)![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點(diǎn),過(guò)點(diǎn)
兩點(diǎn),過(guò)點(diǎn)![]() 的直線(xiàn)交
的直線(xiàn)交![]() 軸負(fù)半軸于
軸負(fù)半軸于![]() ,且
,且![]() .
.
![]() 求點(diǎn)
求點(diǎn)![]() 坐標(biāo).
坐標(biāo).
![]() 求直線(xiàn)
求直線(xiàn)![]() 的解析式.
的解析式.
![]() 直線(xiàn)
直線(xiàn)![]() 的解析式為
的解析式為![]() ,直線(xiàn)
,直線(xiàn)![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,等腰直角三角形OAA1的直角邊OA在x軸上,點(diǎn)A1在第一象限,且OA=1,以點(diǎn)A1為直角頂點(diǎn),OA1為一直角邊作等腰直角三角形OA1A2,再以點(diǎn)A2為直角頂點(diǎn),OA2為直角邊作等腰直角三角形OA2A3…依此規(guī)律,則點(diǎn)A2018的坐標(biāo)是_____.

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com