
【題目】江海化工廠計劃生產甲、乙兩種季節性產品,在春季中,甲種產品售價50千元/件,乙種產品售價30千元/件,生產這兩種產品需要A、B兩種原料,生產甲產品需要A種原料4噸/件,B種原料2噸/件,生產乙產品需要A種原料3噸/件,B種原料1噸/件,每個季節該廠能獲得A種原料120噸,B種原料50噸.
(1)如何安排生產,才能恰好使兩種原料全部用完?此時總產值是多少萬元?
(2)在夏季中甲種產品售價上漲10%,而乙種產品下降10%,并且要求甲種產品比乙種產品多生產25件,問如何安排甲、乙兩種產品,使總產值是1375千元,A,B兩種原料還剩下多少噸?
【答案】(1)生產甲種產品15件,生產乙種產品20件才能恰好使兩種原料全部用完,此時總產值是135萬元;(2)安排生產甲種產品25件,使總產值是1375千元,A種原料還剩下20噸,B種原料正好用完,還剩下0噸.
【解析】分析:(1)可設生產甲種產品x件,生產乙種產品y件,根據等量關系:①生產甲種產品需要的A種原料的噸數+生產乙種產品需要的A種原料的噸數=A種原料120噸,②生產甲種產品需要的B種原料的噸數+生產乙種產品需要的B種原料的噸數=B種原料50噸;依此列出方程求解即可;
(2)可設乙種產品生產z件,則生產甲種產品(z+25)件,根據等量關系:甲種產品的產值+乙種產品的產值=總產值1375千元,列出方程求解即可.
詳解:(1)設生產甲種產品x件,生產乙種產品y件,依題意有:
![]() ,解得
,解得![]() ,
,
15×50+30×20=750+600=1350(千元),1350千元=135萬元.
答:生產甲種產品15件,生產乙種產品20件才能恰好使兩種原料全部用完,此時總產值是135萬元;
(2)設乙種產品生產z件,則生產甲種產品(z+25)件,依題意有:
(1+10%)×50(z+25)+(1﹣10%)×30z=1375,
解得:z=0,z+25=25,120﹣25×4=120﹣100 =20(噸),
50﹣25×2 =50﹣50 =0(噸).
答:安排生產甲種產品25件,使總產值是1375千元,A種原料還剩下20噸,B種原料正好用完,還剩下0噸.


科目:初中數學 來源: 題型:
【題目】水利部門為加強防汛工作,決定對某水庫大壩進行加固,大壩的橫截面是梯形ABCD.如圖所示,已知迎水坡面AB的長為16米,∠B=60°,背水坡面CD的長為 ![]() 米,加固后大壩的橫截面積為梯形ABED,CE的長為8米.
米,加固后大壩的橫截面積為梯形ABED,CE的長為8米.
(1)已知需加固的大壩長為150米,求需要填土石方多少立方米?
(2)求加固后的大壩背水坡面DE的坡度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道對于一個圖形,通過不同的方法計算圖形的面積可以得到一個數學等式.
例如:由圖1可得到(a+b)=a+2ab+b.



圖1 圖2 圖3
(1)寫出由圖2所表示的數學等式:_____________________;寫出由圖3所表示的數學等式:_____________________;
(2)利用上述結論,解決下面問題:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
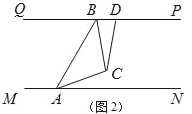
【題目】“一帶一路”讓中國和世界更緊密,“中歐鐵路”為了安全起見在某段鐵路兩旁安置了兩座可旋轉探照燈.如圖1所示,燈A射線從AM開始順時針旋轉至AN便立即回轉,燈B射線從BP開始順時針旋轉至BQ便立即回轉,兩燈不停交叉照射巡視.若燈A轉動的速度是每秒2度,燈B轉動的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若燈B射線先轉動30秒,燈A射線才開始轉動,在燈B射線到達BQ之前,A燈轉動幾秒,兩燈的光束互相平行?
(3)如圖2,若兩燈同時轉動,在燈A射線到達AN之前.若射出的光束交于點C,過C作∠ACD交PQ于點D,且∠ACD=120°,則在轉動過程中,請探究∠BAC與∠BCD的數量關系是否發生變化?若不變,請求出其數量關系;若改變,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為進一步建設秀美、宜居的生態環境,某村欲購買甲、乙、丙三種樹美化村莊,已知甲、乙丙三種樹的價格之比為2:2:3,甲種樹每棵200元,現計劃用210000元資金,購買這三種樹共1000棵.
(1)求乙、丙兩種樹每棵各多少元?
(2)若購買甲種樹的棵樹是乙種樹的2倍,恰好用完計劃資金,求這三種樹各能購買多少棵?
(3)若又增加了10120元的購樹款,在購買總棵樹不變的前提下,求丙種樹最多可以購買多少棵?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠用如圖甲所示的長方形和正方形紙板,做成如圖乙所示的豎式與橫式兩種長方體形狀的無蓋紙盒.

(1)現有正方形紙板162張,長方形紙板340張.若要做兩種紙盒共100個,設做豎式紙盒x個.
①根據題意,完成以下表格:
紙盒 紙板 | 豎式紙盒(個) | 橫式紙盒(個) |
x | 100﹣x | |
正方形紙板(張) | 2(100﹣x) | |
長方形紙板(張) | 4x |
②按兩種紙盒的生產個數來分,有哪幾種生產方案?
(2)若有正方形紙162張,長方形紙板a張,做成上述兩種紙盒,紙板恰好用完.已知290<a<306.求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若正方形EFGH由正方形ABCD繞某點旋轉得到,則可以作為旋轉中心的是( ) 
A.M或O或N
B.E或O或C
C.E或O或N
D.M或O或C
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com