
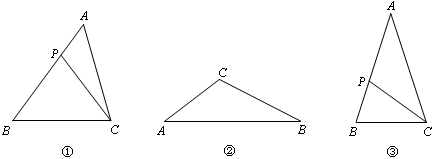
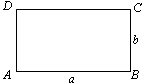
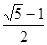 ;(2)①在距離A點b2a處取點P,作PQ⊥CD,垂足為Q;②辯證思考:問題:是不是所有的矩形都存在它的邊上的相似線?如果是,請說明理由;如果不是,請找出一個不存在邊上相似線的矩形.解答:不是,如正方形.
;(2)①在距離A點b2a處取點P,作PQ⊥CD,垂足為Q;②辯證思考:問題:是不是所有的矩形都存在它的邊上的相似線?如果是,請說明理由;如果不是,請找出一個不存在邊上相似線的矩形.解答:不是,如正方形.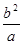 處取點P,作PQ⊥CD,垂足為Q;
處取點P,作PQ⊥CD,垂足為Q;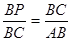 .
.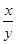 =
=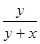 .
.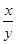 =
=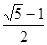 ,即=
,即=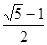 ;
;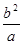 處取點P,作PQ⊥CD,垂足為Q;
處取點P,作PQ⊥CD,垂足為Q;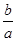 =
=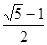 ),PQ為矩形ABCD的邊AB、CD上的相似線,求
),PQ為矩形ABCD的邊AB、CD上的相似線,求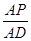 .
.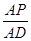 =
=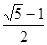 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:不詳 題型:解答題
 ,那么稱點C為線段AB的黃金分割點。某數學興趣小組在進行課題研究時,由黃金分割點聯想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1、S2,如果
,那么稱點C為線段AB的黃金分割點。某數學興趣小組在進行課題研究時,由黃金分割點聯想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1、S2,如果 ,那么稱直線l為該圖形的黃金分割線.
,那么稱直線l為該圖形的黃金分割線.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
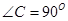 ,AC=8cm,BC=6cm.點P由B出發沿BA方向向點A勻速運動,同時點Q由A出發沿AC方向向點C勻速運動,它們的速度均為2cm/s.以AQ、PQ為邊作平行四邊形AQPD,連接DQ,交AB于點E.設運動的時間為t(單位:s)(0≤t≤4).解答下列問題:
,AC=8cm,BC=6cm.點P由B出發沿BA方向向點A勻速運動,同時點Q由A出發沿AC方向向點C勻速運動,它們的速度均為2cm/s.以AQ、PQ為邊作平行四邊形AQPD,連接DQ,交AB于點E.設運動的時間為t(單位:s)(0≤t≤4).解答下列問題: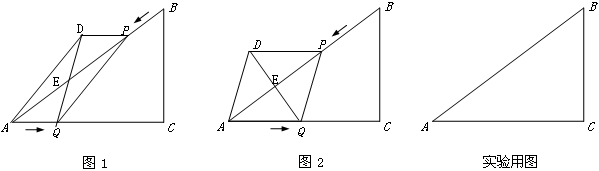
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 . 過點A作BC的平行線與∠ABC的平分線交于點D,連接CD.
. 過點A作BC的平行線與∠ABC的平分線交于點D,連接CD. 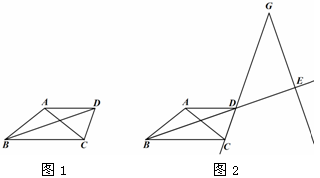
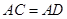 ;
; 為線段
為線段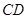 延長線上一點,將射線GC繞著點G逆時針旋轉
延長線上一點,將射線GC繞著點G逆時針旋轉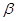 ,與射線BD交于點E.
,與射線BD交于點E. ,
, ,如圖2所示,求證:
,如圖2所示,求證: ;
; ,
, ,請直接寫出
,請直接寫出 的值(用含
的值(用含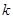 的代數式表示).
的代數式表示).查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
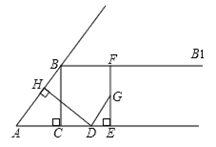
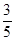 時,連結C ′C,則以CC´為直徑的圓何時與直線AB相切?
時,連結C ′C,則以CC´為直徑的圓何時與直線AB相切?查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com