【題目】在2019年10月1日的建國70周年慶典上，有多國領導人出席觀看了我國盛大的閱兵儀式.為表示友好，我國政府選擇將刺繡和陶瓷兩類工藝品作為國禮贈送給所有的來賓.甲，乙兩個工廠分別承接了制作
，
兩種刺繡與
種陶瓷的任務.甲工廠安排100名工人制作刺繡，每人只能制作其中一種刺繡，乙工廠安排50名工人制作種陶瓷.的人均制作數量比的人均制作數量少3件，的人均制作量比的人均制作量少20%.若本次贈送的國禮（，，三樣禮品）的人均制作數量比的人均制作數量少30%，且的人均制作數量為偶數件，則本次贈送的國禮共制作了_________件.
孟建平小學滾動測試系列答案
黃岡天天練口算題卡系列答案科目：初中數學 來源： 題型：
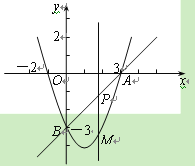
【題目】如圖，在平面直角坐標系中，拋物線y＝x2＋mx＋n經過點A(3，0)、
B(0，－3)，點P是直線AB上的動點，過點P作x軸的垂線交拋物線于點M，設點P的橫
坐標為t．
(1)分別求出直線AB和這條拋物線的解析式．
(2)若點P在第四象限，連接AM、BM，當線段PM最長時，求△ABM的面積．
(3)是否存在這樣的點P，使得以點P、M、B、O為頂點的四邊形為平行四邊形？若存在，請直接寫出點P的橫坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，⊙O的半徑為1，A，P，B，C是⊙O上的四個點．∠APC=∠CPB=60°．
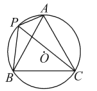
（1）判斷△ABC的形狀： ；
（2）試探究線段PA，PB，PC之間的數量關系，并證明你的結論；
（3）當點P位于
的什么位置時，四邊形APBC的面積最大？求出最大面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，BC是半⊙O的直徑，點P是半圓弧的中點，點A是弧BP的中點，AD⊥BC于D，連結AB、PB、AC，BP分別與AD、AC相交于點E、F．
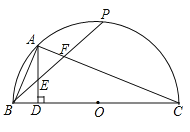
（1）求證：AE=BE；
（2）判斷BE與EF是否相等嗎，并說明理由；
（3）小李通過操作發現CF=2AB，請問小李的發現是否正確？若正確，請說明理由；若不正確，請寫出CF與AB正確的關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】初中數學代數知識中，方程、函數、不等式存在著緊密的聯系，請閱讀下列兩則材料，回答問題：
利用函數圖象找方程
解的范圍.設函數
，當
時，
；當
時，
.則函數
的圖象經過兩個點
與
，而點在
軸下方，點在軸上方，則該函數圖象與軸交點橫坐標必大于-2，小于-1.故，方程的有解，且該解的范圍為
.
材料二：
解一元二次不等式
.由“異號兩數相乘，結果為負可得：
情況①
，得
，則
情況②
，得
，則無解
故，的解集為.
（1）請根據材料一解決問題：已知方程
有唯一解
，且
（
為整數），求整數的值.
（2）請結合材料一與材料二解決問題：若關于的方程
的解分別為
，
，且
，
，求
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，O為坐標原點，已知點F（2
，0），直線GF交y軸正半軸于點G，且∠GFO=30°．
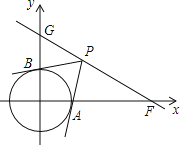
（1）直接寫出點G的坐標；
（2）若⊙O的半徑為1，點P是直線GF上的動點，直線PA、PB分別約⊙O相切于點A、B．
①求切線長PB的最小值；
②問：在直線GF上是夠存在點P，使得∠APB=60°，若存在，請求出P點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
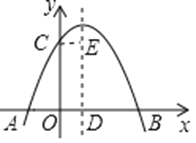
【題目】如圖，拋物線y＝ax2+bx+c（a≠0）與y軸交于點C，與x軸交于A，B兩點，其中點B的坐標為B（4，0），拋物線的對稱軸交x軸于點D，CE∥AB，并與拋物線的對稱軸交于點E．現有下列結論：①a＞0；②b＞0；③4a+2b+c＜0；④AD+CE＝4．其中所有正確結論的序號是 _____________________ ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
