
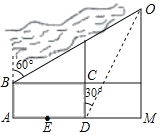
【題目】如圖所示,小亮家在點O處,其所在學校的校園為矩形ABCD,東西長AD=1000米,南北長AB=600米.學校的南正門在AD的中點E處,B為學校的西北角門.小亮從家到學校可以走馬路,路線O→M→E(∠M=90°);也可以走沿河觀光路,路線O→B.小亮在D處測得O位于北偏東30°,在B處測得O位于北偏東60°小亮從家到學校的兩條路線中,長路線比短路線多_____米.(結果保留根號)
【答案】![]()
【解析】
如圖,由題意得,∠OBF=30°,DOM=30°,FM=AB=600,設DM=CF=x,得到BF=1000+x,解直角三角形即可得到結論.
解:如圖,由題意得,∠OBF=30°,DOM=30°,FM=AB=600,
設DM=CF=x,
則BF=1000+x,
在Rt△BOF中,∵∠OBF=30°,
∴OF=![]() BF=
BF=![]() ,OB=
,OB= ,
,
在Rt△ODM中,DM=x,
∴OM=![]() x,
x,
∴OF=OM﹣FM=![]() x﹣600,
x﹣600,
∴![]() =
=![]() x﹣600,
x﹣600,
解得:x=500+300![]() ,
,
∴OF=500![]() +300,
+300,
∴BO=2OF=1000![]() +600,
+600,
∴路線O→M→E的長度=500+x+![]() x=500+500+300
x=500+500+300![]() +500
+500![]() +900=1900+800
+900=1900+800![]() ,
,
∴長路線比短路線多(1300﹣200![]() )米,
)米,
故答案為:1300﹣200![]() .
.



 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:
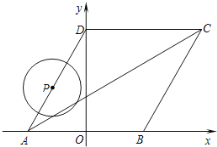
【題目】如圖所示,菱形ABCD的頂點A、B在![]() 軸上,點A在點B的左側,點D在
軸上,點A在點B的左側,點D在![]() 軸的正半軸上,
軸的正半軸上,![]() ,點A的坐標為
,點A的坐標為![]() .
.
(1)求D點的坐標.
(2)求直線AC的函數關系式.
(3)動點P從點A出發,以每秒1個單位長度的速度,按照![]() 的順序在菱形的邊上勻速運動一周,設運動時間為
的順序在菱形的邊上勻速運動一周,設運動時間為![]() 秒.求
秒.求![]() 為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,D是![]() 的中點,E為OD延長線上一點,且∠CAE=2∠C,AC與BD交于點H,與OE交于點F.
的中點,E為OD延長線上一點,且∠CAE=2∠C,AC與BD交于點H,與OE交于點F.
(1)求證:AE是⊙O的切線;
(2)若DH=9,tanC=![]() ,求直徑AB的長.
,求直徑AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,點F為BE的中點,連接CF,DF.

(1)如圖1,當點D在AB上,點E在AC上時
①證明:△BFC是等腰三角形;
②請判斷線段CF,DF的關系?并說明理由;
(2)如圖2,將圖1中的△ADE繞點A旋轉到圖2位置時,請判斷(1)中②的結論是否仍然成立?并證明你的判斷.
查看答案和解析>>
科目:初中數學 來源: 題型:
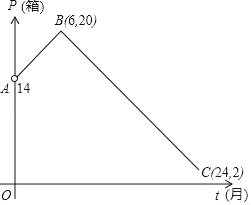
【題目】某竹制品加工廠根據市場調研結果,對該廠生產的一種新型竹制品玩具未來兩年的銷售進行預測,并建立如下模型:設第t個月,竹制品銷售量為P(單位:箱),P與t之間存在如圖所示函數關系,其圖象是線段AB(不含點A)和線段BC的組合.設第t個月銷售每箱的毛利潤為Q(百元),且Q與t滿足如下關系Q=2t+8(0≤t≤24).
(1)求P與t的函數關系式(6≤t≤24).
(2)該廠在第幾個月能夠獲得最大毛利潤?最大毛利潤是多少?
(3)經調查發現,當月毛利潤不低于40000且不高于43200元時,該月產品原材料供給和市場售最和諧,此時稱這個月為“和諧月”,那么,在未來兩年中第幾個月為和諧月?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某新建火車站站前廣場需要綠化的面積為46000米2,施工隊在綠化了22000米2后,將每天的工作量增加為原來的1.5倍,結果提前4天完成了該項綠化工程.
(1)該項綠化工程原計劃每天完成多少米2?
(2)該項綠化工程中有一塊長為20米,寬為8米的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為56米2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),問人行通道的寬度是多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某店因為經營不善欠下68400元的無息貸款的債務,想轉行經營服裝專賣店又缺少資金.“中國夢想秀”欄目組決定借給該店30000元資金,并約定利用經營的利潤償還債務(所有債務均不計利息).已知該店代理的品牌服裝的進價為每件40元,該品牌服裝日銷售量![]() (件)與銷售價
(件)與銷售價![]() (元件)之間的關系可用圖中的一條折線(實線)來表示.該店應支付員工的工資為每人每天82元,每天還應支付其它費用為106元(不包含債務).
(元件)之間的關系可用圖中的一條折線(實線)來表示.該店應支付員工的工資為每人每天82元,每天還應支付其它費用為106元(不包含債務).
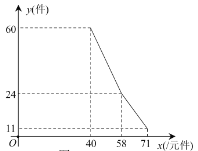
(1)求日銷售量![]() (件)與銷售價
(件)與銷售價![]() (元/件)之間的函數關系式;
(元/件)之間的函數關系式;
(2)若該店暫不考慮償還債務,當某天的銷售價為48元/件時,當天正好收支平衡(收入=支出),求該店員工的人數;
(3)若該店只有2名員工,則該店最早需要多少天能還清所有債務,此時每件服裝的價格應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
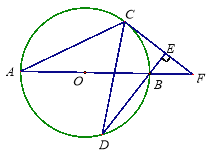
【題目】如圖,AB為⊙O直徑,C、D為⊙O上不同于A、B的兩點,∠ABD=2∠BAC,連接CD.過點C作CE⊥DB,垂足為E,直線AB與CE相交于F點.
(1)求證:CF為⊙O的切線;
(2)當BF=5,![]() 時,求BD的長.
時,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
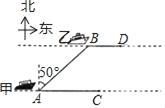
【題目】如圖,海面上甲、乙兩船分別從A,B兩處同時出發,由西向東行駛,甲船的速度為24n mile/h,乙船的速度為15n mile/h,出發時,測得乙船在甲船北偏東50°方向,且AB=10nmile,經過20分鐘后,甲、乙兩船分別到達C,D兩處.
(參考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求兩條航線間的距離;
(2)若兩船保持原來的速度和航向,還需要多少時間才能使兩船的距離最短?(精確到0.01)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com