【題目】已知：如圖，在
中，
，
，
．點
從點
開始沿
邊向點
以
的速度移動，同時點
從點開始沿
邊向點
以
的速度移動．當一個點到達終點時另一點也隨之停止運動，設運動時間為
秒，
求幾秒后，
的面積等于
？
求幾秒后，
的長度等于
？
運動過程中，
的面積能否等于
？說明理由．
【答案】（1）
或
秒后
的面積等于
；（2）當
或時，
的長度等于
；（3）
的面積不能等于
．
【解析】
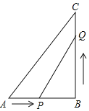
（1）設經過x秒鐘，△PBQ的面積等于6平方厘米，根據點P從A點開始沿AB邊向點B以1cm/s的速度移動，點Q從B點開始沿BC邊向點C以2cm/s的速度移動，表示出BP和BQ的長可列方程求解．
（2）根據PQ=5，利用勾股定理BP2+BQ2=PQ2，求出即可；
（3）通過判定得到的方程的根的判別式即可判定能否達到8cm2．
(1)設經過x秒以后△PBQ面積為6
×(5x)×2x=6
整理得：x25x+6=0
解得：x=2或x=3
答：2或3秒后△PBQ的面積等于6cm2.
當
時，在
中，∵
，
∴
，
，
，
，
，
∴當或時，的長度等于．
設經過
秒以后面積為
，
整理得：
∴的面積不能等于．
科目：初中數學 來源： 題型：
【題目】已知△ABC是等邊三角形，點D，E分別為邊AB，AC上的點，且有AE＝DB，連接DE，DC．
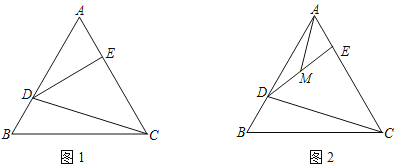
（1）如圖1，若AB＝6，∠DEC＝90°，求△DEC的面積．
（2）M為DE中點，當D，E分別為AB、AC的中點時，判定CD，AM的數量關系并說明理由．
（3）如圖2，M為DE中點，當D，E分別為AB，AC上的動點時，判定CD，AM的數量關系并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一元二次方程2x2+2x﹣1=0的兩個根為x1，x2，且x1＜x2，下列結論正確的是（ ）
A. x1+x2=1 B. x1x2=﹣1 C. |x1|＜|x2| D. x12+x1=
查看答案和解析>>
科目：初中數學 來源： 題型：
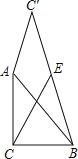
【題目】如圖，已知△ABC中，∠ACB=90°，AC=BC=2，將直角邊AC繞A點逆時針旋轉至AC′，連接BC′，E為BC′的中點，連接CE,則CE的最大值為( ).
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題探究：已知平行四邊形
的面積為
，
是
所在直線上一點．
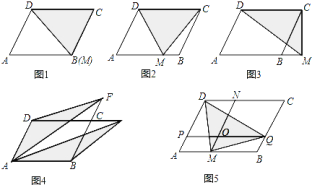
如圖
：當點與
重合時，
________；
如圖
，當點與與
均不重合時，________；
如圖
，當點在（或
）的延長線時，________．
拓展推廣：如圖
，平行四邊形的面積為
，
、
分別為
、
延長線上兩點，連接
、
、
、
，求出圖中陰影部分的面積，并說明理由．
實踐應用：如圖是一平行四邊形綠地，
、
分別平行于、
，它們相交于點
，
，
，
，
，現進行綠地改造，在綠地內部作一個三角形區域
（連接
、
、
，圖中陰影部分）種植不同的花草，求出三角形區域的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，BD是AC邊上的中線，AE⊥BC，垂足為點E，交BD于F，cos∠ABC=
，AB=13．
（1）求AE的長；
（2）求tan∠DBC的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，過點A作AE⊥BC，垂足為E，連接DE，F為線段DE上一點，且∠AFE=∠B
（1）求證：△ADF∽△DEC；
（2）若AB=8，AD=6
，AF=4，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，P是等邊三角形ABC內的一點，且PA=3，PB=4，PC=5，將△ABP繞點B順時針旋轉60°到△CBQ位置．連接PQ，則以下結論錯誤的是（ ）
A. ∠QPB=60° B. ∠PQC=90° C. ∠APB=150° D. ∠APC=135°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
